K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

10 tháng 6 2016
Tần số: \(f=\dfrac{1}{2\pi\sqrt {LC}}\Rightarrow f^2=\dfrac{a}{C}\) (a là 1 hằng số nào đó, do bài này f chỉ phụ thuộc vào C)
\(\Rightarrow f_1^2=\dfrac{a}{C_1}\)
\(f_2^2=\dfrac{a}{C_2}\)
Cần tìm: \(\Rightarrow f^2=\dfrac{a}{C}=a.(\dfrac{1}{C_1}+\dfrac{1}{C_2})=f_1^2+f_2^2\)
\(\Rightarrow f=\sqrt{30^2+40^2}=50(Hz)\)
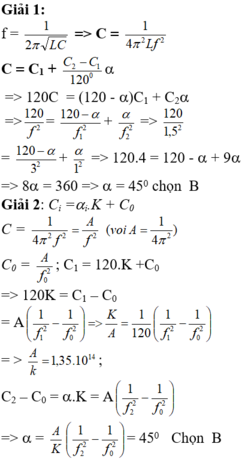
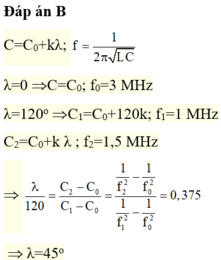
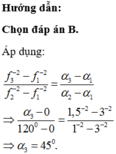
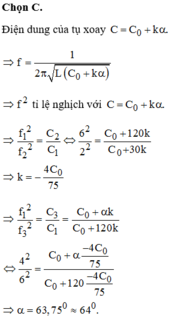
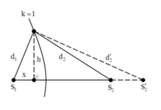
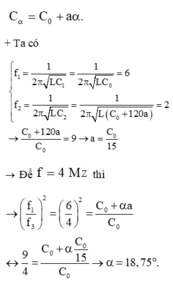

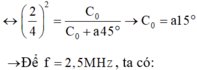
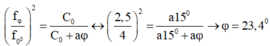
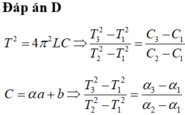
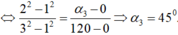
\(f=\frac{1}{2\pi\sqrt{LC}}\rightarrow C=\frac{1}{4\pi^2Lf^2}\) \(C=C_1+\frac{C_2-C_1}{120^o}\alpha\rightarrow120C\)\(=\left(120-\alpha\right)C_1+C_2\alpha\)
\(\rightarrow\frac{120}{f^2}=\frac{120-\alpha}{f^2_1}+\frac{\alpha}{f_2^2}\rightarrow\)\(\frac{120}{1,5^2}=\frac{120-\alpha}{3^2}+\frac{\alpha}{1^2}\rightarrow120.4=120-\alpha+9\alpha\)
\(\rightarrow8\alpha=360\rightarrow\alpha=45^o\)
Đáp án D