Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Thế năng đàn hồi : Thế năng đàn hồi :
Cách giải:
Độ dãn của lò xo tại vị trí cân bằng: ![]()
Biên độ dao động của con lắc: A = 7,5 - Δl0 = 7,5 - 2,5 = 5cm
Ta có: Δl0< A
Chọn chiều dương hướng xuống
=> Vị trí lực đàn hồi có độ lớn nhỏ nhất là vị trí lò xo hông giãn cũng hông nén: Δl = 0
Thế năng đàn hồi tại vị trí đó: 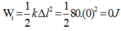

Thiếu m hoặc \(\omega\),
Hướng dẫn: Từ \(F_{dh}\le1,5\) suy ra miền giá trị của li độ \(x\), từ đó tìm ra thời gian bạn nhé.


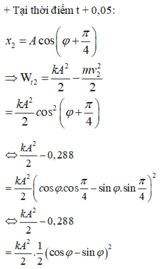


Thời gian lò xo giãn trong một chu kì được biểu diễn trên đường tròn lượng giác:

Đáp án D

Chu kì dao động: T = 2π/ω = 2π/5π = 0,4s
Thời điểm t = 0 và thời điểm độ lớn lực đàn hồi bằng 0,5N được biểu diễn trên đường tròn lượng giác:
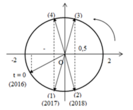
Một chu kì có 4 lần độ lớn lực đàn hồi bằng 0,5N
Sau 504T độ lớn lực đàn hồi bằng 0,5N lần thứ 2016
=> Lực đàn hồi có độ lớn bằng 0,5N lần thứ 2018 vào thời điểm:
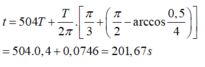
Đáp án C

Ta có:\(\Delta\)l=4cm;A=8cm;T=2\(\pi\)\(\sqrt{\frac{\Delta l}{g}}\)=0,4(s)
2\(\alpha\)=\(\omega\)\(\Delta\)t nén
\(\Rightarrow\)\(\Delta\)t nén =\(\frac{2\alpha}{\omega}\)=\(\frac{2arccos\frac{\Delta l}{A}}{\frac{2\pi}{T}}\)=\(\frac{2.\frac{\pi}{3}}{2\pi}\).o,4=\(\frac{2}{15}\)(s)
Có j sai sót mong mn giúp đỡ![]()

Biên độ: \(A=10cm\)
Tần số góc: \(\omega=10(rad/s)\)
Tại vị trí lò xo bị giãn \(5cm\) thì li độ của vật là: \(x=-10+5=-5cm\)
Vật đang đi lên là chuyển động theo chiều âm.
\(\Rightarrow \cos\varphi=-\dfrac{5}{10}=-0,5\)
\(\Rightarrow \varphi = \dfrac{2\pi}{3}\) (rad) (vì vật chuyển động theo chiều âm nên \(\varphi < 0\) )
PT dao động: \(x=10\cos(10t+\dfrac{2\pi}{3}) (cm)\)
Ở VTCB lò xo giãn 10 cm, như vậy để nó giãn 5cm thì từ VTCB phải đi lên 5cm.
Chiều dương hướng xuống, nên li độ lúc đó phải bằng -5cm.
O -5cm -10cm Lò xo không biến dạng Lò xo giãn 5cm Lò xo giãn 10cm x