Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có 7 trận: Tứ kết 1, Tứ kết 2, Tứ kết 3, Tứ kết 4, Bán kết 1, Bán kết 2, Chung kết.

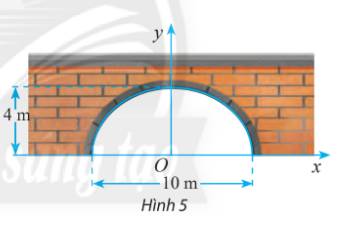
Chiều cao là 4 m tương ứng với \(b = 4\)
Chiều rộng bằng 10 m nên \(2a = 10 \Rightarrow a = 5\)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)

Gọi phương trình chính tắc của parabol là: \({y^2} = 2px\left( {p > 0} \right)\)
Vì \(AB = 40cm\) và \(h = 30cm\) nên \(A\left( {30;20} \right)\)
Do \(A\left( {30;20} \right)\) thuộc parabol nên ta có: \({20^2} = 2p.30 \Rightarrow p = \frac{{20}}{3}\)
Vậy parabol có phương trình chính tắc là: \({y^2} = \frac{{40}}{3}x\)

Kết quả của mỗi lần thử là một cặp (i; j) với i và j lần lượt là số chấm xuất hiện trên hai xúc xắc, hai con xúc xắc gieo đồng thời nên không quan tâm thứ tự, ta có không gian mẫu là:
\(\Omega = \begin{array}{l}\{(1;1),(1;2),(1;3),(1;4),(1;5),(1;6),(2;2),(2;3),(2;4),(2;5),(2;6),(3;3),(3;4),(3;5),(3;6),\\(4;4),(4;5),(4;6),(5;5),(5;6),(6;6)\}\end{array} \)
Không gian mẫu gồm có 21 kết quả, tức là \(n\left( \Omega \right) = 21\)
a) Ta có tập hợp miêu tả biến cố A
\(A = \left\{ {(1;1),(2;2),(3;3),(4;4),(5;5),(6;6)} \right\} \Rightarrow n\left( A \right) = 6\)
Do đó, xác suất của biến cố A là: \(P\left( A \right) = \frac{{n(A)}}{{n(\Omega )}} = \frac{6}{{21}} = \frac{2}{7}\)
b) Ta có tập hợp miêu tả biến cố B
\(B = \left\{ {(6;3),(5;4)} \right\} \Rightarrow n\left( B \right) = 2\)
Do đó, xác suất của biến cố B là: \(P\left( B \right) = \frac{{n(B)}}{{n(\Omega )}} = \frac{2}{{21}}\)

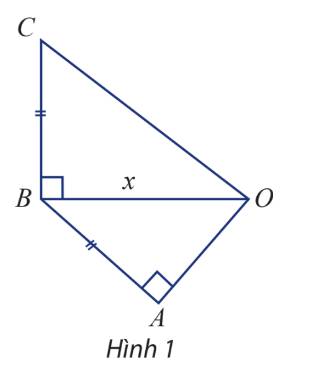
Gọi độ dài cạnh OB là x cm \(\left( {x > 0} \right)\)
Theo giả thiết ta có \(AB = BC = OB - 1 = x - 1\)
Áp dụng định lý pitago trong tam giác vuông OAB và OBC ta có:
\(OC = \sqrt {O{B^2} + B{C^2}} = \sqrt {{x^2} + {{\left( {x - 1} \right)}^2}} = \sqrt {2{x^2} - 2x + 1} \)
\(OA = \sqrt {O{B^2} - A{B^2}} = \sqrt {{x^2} - {{\left( {x - 1} \right)}^2}} = \sqrt {2x - 1} \)
a) \(OC = 3OA \Rightarrow \sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = 9\left( {2x - 1} \right)\\ \Rightarrow 2{x^2} - 20x + 10 = 0\end{array}\)
\( \Rightarrow \)\(x = 5 - 2\sqrt 5 \) và \(x = 5 + 2\sqrt 5 \)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \) ta thấy cả hai đều thỏa mãn phương trình
Vậy khi \(OB = 5 - 2\sqrt 5 \) hoặc \(OB = 5 + 2\sqrt 5 \)thì \(OC = 3OA\)
b) \(OC = \frac{5}{4}OB \Rightarrow \sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = \frac{{25}}{{16}}{x^2}\\ \Rightarrow \frac{7}{{16}}{x^2} - 2x + 1 = 0\end{array}\)\(\)
\( \Rightarrow x = \frac{4}{7}\) hoặc \(x = 4\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\) ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy khi \(OB = \frac{4}{7}\) hoặc \(OB = 4\) (cm) thì \(OC = \frac{5}{4}OB\)

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)

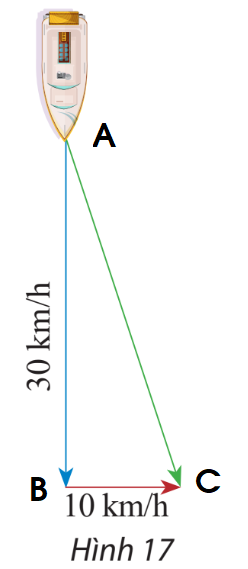
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).

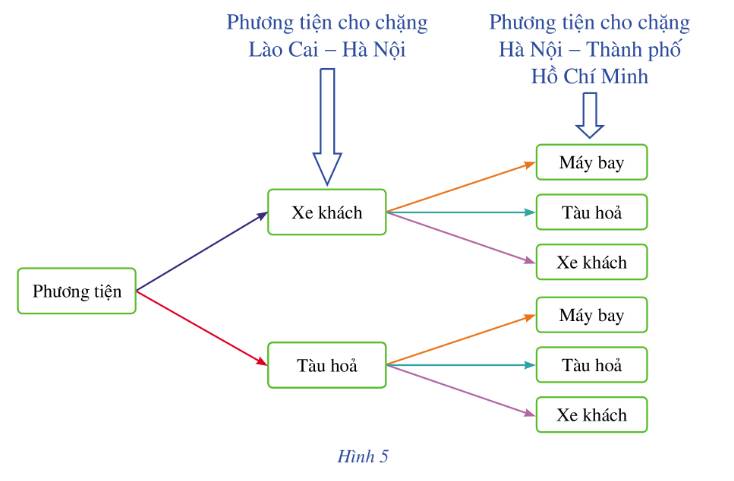
Có 6 cách chọn phương tiện đi từ Lào Cai đến Thành phố Hồ Chí Minh, qua Hà Nội.
Xe khách, Máy bay
Xe khách, Tàu hỏa
Xe khách, Xe khách
Tàu hỏa, Máy bay
Tàu hỏa, Tàu hỏa
Tàu hỏa, Xe khách
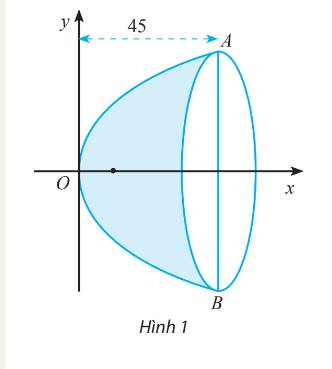




Từ giả thiết ta có tiêu điểm \(F(5;0)\), suy ra \(\frac{p}{2} = 5\) hay \(p=10\).
Vậy phương trình chính tắc của parabol là: \({y^2} = 20x\)
Chiều sâu của gương là 45 cm tương ứng với \({x_A} = 45\), thay \({x_A} = 45\) vào phương trình \({y^2} = 20x\) ta có: \({y^2} = 20.45 = 900 \Rightarrow {y_A} = 30 \Rightarrow AB = 2{y_A} = 60 \)
Vậy khoảng cách AB là \(60 cm\)