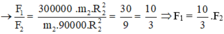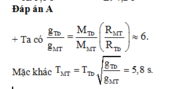Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Chu kì của con lắc ở mặt đất là: T = 2 π l g với g = G M R 2
Chu kì của con lắc ở độ cao h là T’: T’ = 2 π l g h với gh = G M ( R + h ) 2
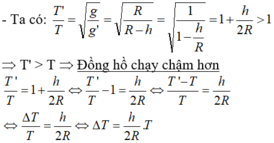
Lập tỷ lệ: T ' T = g g h = R + h R = 1 + h R > 1 ⇒ T ' > T Þ Đồng hồ chạy chậm hơn so với ở mặt đất
Mỗi chu kì đồng hồ sai thời gian ΔT:
∆ T T 1 = T 2 - T 1 T 1 = h R ⇒ ∆ T = T 1 h R
Do ΔT > 0 đồng hồ chạy chậm và mỗi ngày chậm:
ζ = n . ∆ T = 24 . 3600 T 1 . T 1 . 0 , 64 6400 = 86400 . 10 - 4 = 8 , 64 ( s )

Chạy đúng: \(T=2\pi\sqrt{\dfrac{l}{g}}\)
Chạy sai: \(T'=2\pi\sqrt{\dfrac{l}{g\prime}}\), Với gia tốc trọng trường \(g'=g(\dfrac{R}{R+h})^2\)
Tỷ số: \(\dfrac{T'}{T}=\dfrac{g'}{g}=\dfrac{R}{R+h} <1\) nên đồng hồ chạy nhanh.
Một ngày đêm sẽ nhanh
\(\Delta t= 24.60.60.\mid\dfrac{T\prime}{T}-1\mid=24.60.60.\dfrac{h}{R+h}=67,45 (s)\approx68(s)\)
Bạn ơi mình chắc chắn là chạy chậm hơn vì càng cách xa mặt đất thì áp suất càng thấp quả lắc sẽ nhẹ hơn nên dao động sẽ chậm hơn. Dù sao cũng cảm ơn bạn nhiều ^^

Ta có hệ:
\(\left\{{}\begin{matrix}1,9=2\pi\sqrt{\dfrac{l}{g}}\\T_h=2\pi\sqrt{\dfrac{l}{g_h}}\end{matrix}\right.\)
Xét tỉ lệ:
\(\Rightarrow\dfrac{T_h}{1,9}=\sqrt{\dfrac{G\cdot\dfrac{M}{R^2}}{G\cdot\dfrac{M'}{\left(R+h\right)^2}}}=\sqrt{\dfrac{\dfrac{81M'}{\left(3,7R'\right)^2}}{\dfrac{M'}{R'^2}}}\)
\(\Rightarrow T_h=4,62s\)

Chọn D
- Khối lượng trái đất là: 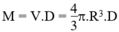 với R là bán kính trái đất
với R là bán kính trái đất
- Khối lượng phần trái đất tính từ độ sâu h đến tâm là:
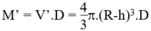
- Gia tốc trọng trường trên mặt đất là: 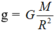
- Gia tốc trọng trường ở độ sâu h là: 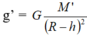
- Gọi T là chu kì của con lắc trên mặt đất là: 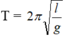
- Gọi T’ là chu kì của con lắc ở độ sâu h là T’: 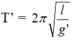
+ Do ΔT > 0 đồng hồ chạy chậm và một tuần lễ chậm:
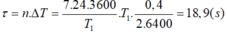

Chọn đáp án D.
Gọi: R1 là khoảng cách từ Mặt Trời đến Mặt Trăng.
R2 là khoảng cách từ Trái Đất đến Mặt Trời
m là khối lượng của Mặt Trăng.
m1 là khối lượng của Mặt Trời
m2 là khối lượng của Trái Đất
Lực hấp dẫn do Mặt Trời tác dụng lên Mặt Trăng: 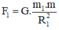
Lực hấp dẫn do Mặt Trăng tác dụng lên Mặt Trời: 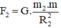
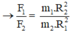
Mà R1 = 300R2; m1 = 300000 m2