Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đầu tiên ta chọn 4 nam, 1 nữ cho tỉnh thứ nhất. Theo quy tắc nhân số cách chọn là
\(n_1\) = \(C_{12}^4\).\(C_3^1\) = 1485
Sau đó chọn 4 nam và 1 nữ cho tỉnh thứ hai, 4 nam sẽ được chọn trong 8 nam còn lại, 1 nữ sẽ chọn trong 2 nữ còn lại. Vậy theo quy tắc nhân số cách chọn là
\(n_2\) = \(C_8^4\).\(C_2^1\) = 140
Còn lại ta chọn cho tỉnh thứ ba
Lại theo quy tắc nhân, số cách phân công là
n=\(n_1\).\(n_2\) = 1485 x 140 = 207900.

Bước 1: Chọn 4 nam và 1 nữ về tỉnh thứ nhất, có ![]() cách.
cách.
Bước 2: Chọn 4 nam từ 8 nam còn lại, 1 nữ từ 2 nữ còn lại về tỉnh thứ hai, có ![]() cách.
cách.
Bước 3: Phân công 4 nam còn lại và 1 nữ còn lại về tỉnh thứ 3, có 1 cách.
Vậy theo quy tắc nhân, số cách phân công sẽ là: ![]() = 207900.
= 207900.
Chọn A.

Có C 12 4 cách phân công 4 nam về tỉnh thứ nhất
Với mỗi cách phân công trên thì có C 8 4 cách phân công 4 nam về tỉnh thứ hai và có C 4 4 cách phân công 4 nam còn lại về tỉnh thứ ba.
Khi phân công nam xong thì có 3! cách phân công ba nữ về ba tỉnh đó.
Vậy có tất cả C 12 4 . C 8 4 . C 4 4 . 3 ! = 4989600 cách phân công.
Chọn đáp án C.

Đáp án là D
Nhóm thứ 1: chọn 7 nam từ 21 bạn nam, chọn 5 nữ từ 15 bạn nữ nên số cách chọn nhóm thứ nhất là: C 21 7 . C 15 5 cách.
Nhóm thứ 2: chọn 7 nam từ 14 bạn nam còn lại, chọn 5 nữ từ 10 bạn nữ còn lại nên số cách chọn nhóm thứ hai là: C 14 7 . C 10 5 cách.
Số cách chọn nhóm thứ ba là: C 7 7 . C 5 5 cách.
Vậy có C 21 7 . C 15 5 x ( C 14 7 . C 10 5 ) x ( C 7 7 . C 4 5 ) = C 21 7 C 15 5 C 14 7 C 10 5 cách chia nhóm.

Chọn 4 trong 15 bạn là tổ hợp chập 4 của 15 nên ta có:
\(C^4_{15}=1365\) cách chọn

Đáp án D
Chọn 4 học sinh bất kỳ có: Ω = C 13 4 = 715
Gọi A là biến cố: “4 học sinh được chọn có đủ 3 khối”
Khi đó
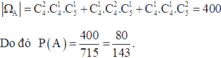



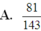
Có C31 .C124 cách phân công thanh niên về tỉnh thứ nhất. Với mỗi cách này thì có C21 .C84 cách phân công số thanh niên còn lại về tỉnh thứ hai. Với mỗi cách phân công về hai tỉnh trên thì có C11 .C44 cách phân công về tỉnh thứ ba.
Do đó có C31 .C124 .C21 .C84 . C11 .C44 =207900 cách
Chọn C