Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi thời gian dự định hoàn thành công việc là x (ngày) (x > 2)
DKXD: x thuoc N*
Diện tích ruộng mà đội phải cày theo kế hoạch là 40x (ha)
Thời gian thực tế đội đã làm để hoàn thành công việc là x – 2 (ngày)
Diện tích ruộng đội đã cày được theo thực tế là: 52(x – 2)
Theo bài ra ta có phương trình:
40x + 4 = 52(x – 2)
⇔ 40x + 4 = 52x – 104
⇔ 12x = 108
⇔ x = 9 (tmđk)
Vậy diện tích ruộng đội phải cày theo kế hoạch là 40.9 = 360ha.

Gọi x (tấn) là lượng than mà đội khai thác mỗi ngày theo kế hoạch. Điều kiện: x > 0
Sau 3 ngày đầu, mỗi ngày đội khai thác (x + 8) tấn
Thời gian dự định khai thác là 216/x (ngày)
Lượng than khai thác 3 ngày đầu là 3x (tấn)
Lượng than khai thác trong những ngày còn lại là 232 – 3x (tấn)
Thời gian đội khai thác 232 – 3x tấn than là (232 - 3x)/(x + 8) (ngày)
Theo đề bài, ta có phương trình:
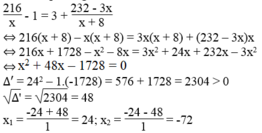
Giá trị x = -72 không thỏa mãn điều kiện bài toán.
Vậy theo kế hoạch mỗi ngày đội khai thác 24 tấn than.

gọi x là số sản phẩm làm 1 ngày theo dự định
3200/x là số ngày làm 3200 sp theo dự định
5+(3200-5x)/(x+40) là số ngày làm xong sản phẩm thực tê
ta có pt
3200/x-3=(5+(3200-5x)/(x+40))

Gọi số sản phẩm đội dự định làm mỗi ngày là x (x ∈ ℕ * , x < 84) (sản phẩm)
*) Theo kế hoạch, thời gian hoàn thành là 1000/x (ngày)
*) Thực tế, mỗi ngày làm được x + 10 (sản phẩm)
Thời gian hoàn thành 1000/(x+10) (ngày)
Vì thời gian thực tế ít hơn thời gian dự định là 2 ngày nên ta có phương trình:
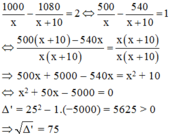
Phương trình có hai nghiệm phân biệt: x 1 = − 25 – 75 = −100 (loại)
và x 2 = −25 + 75 = 50 (tmđk)
Vậy theo kế hoạch, mỗi ngày tổ dự định làm 50 sản phẩm
Đáp án: C

Giải
Gọi khối lượng hàng chở theo định mức trong 1 ngày của đội là x ( tấn ) ( x > 0)
Số ngày quy định là \(\frac{140}{x}\)( ngày )
Do vượt mức nên số ngày đội đã chở là \(\frac{140}{x}\)= \(1\)( ngày)
Khối lượng hàng đội đã chở được là \(140\)+\(10\)= \(150\) ( tấn )
Theo đề bài ta có phương trình:
<=> ( \(\frac{140}{x}\)- \(1\)) ( \(x\)+ \(5\)) = \(140\)+ \(10\)
<=> (\(140\)- \(x\)) ( \(x\)+ \(5\)) = \(150x\)
<=> \(140x\)+ \(700\)- \(5x\)- X2
<=> X2 + \(15x\)- \(700\)= \(0\)
Giải ra \(x\)= \(20\)( T/M) và \(x\)= - \(35\)( loại )
Vậy số ngày đội phải chở theo kế hoạch là : \(140\): \(20\)= \(7\)( ngày )
Đáp số : \(7\)ngày.


