Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chu kì của dao động T = 2 π m k = 2 π 0 , 2 10 = 0 , 89 s
+ Độ biến dạng của lò xo tại các vị trí cân bằng tạm x 0 = μ m g k = 0 , 1.0 , 2.10 10 = 2 c m
→ Biên độ dao động của vật trong nửa chu kì đầu tiên là A 1 = X 0 – x 0 = 6 – 2 = 4 c m .
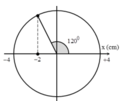
+ Lực đàn hồi của lò xo là nhỏ nhất khi vật đi qua vị trí lò xo không biến dạng, trong nửa chu kì đầu tiên đối vị trí cân bằng tạm O 1 thì vị trí lò xo không biến dạng có li độ x = –2 cm.
→ Thời gian tương ứng Δ t = 120 0 360 0 T = 0 , 296 s
Đáp án A

Hướng dẫn: Chọn đáp án D
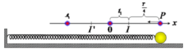
Khoảng cách:
![]()
Thời gian ngắn nhất vật đi từ P đến điểm O là
![]()
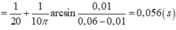
Tốc độ trung bình trong khoảng thời gian đó:
![]()

Hướng dẫn:
Độ biến dạng của lò xo tại các vị trí cân bằng tạm x 0 = μ m g k = 0 , 5.0 , 3.10 300 = 0 , 5 c m
+ Biên độ dao động của vật trong nửa chu kì đầu tiên A 1 = X 0 – x 0 = 5 – 0 , 5 = 4 , 5 c m .
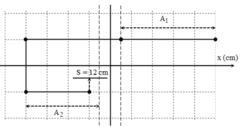
+ Biên độ dao động của vật trong nửa chu kì tiếp theo A 2 = A 1 – 2 x 0 = 4 , 5 – 1 = 3 , 5 c m → sau khi đi được quãng đường 12 cm, vật đến vị trí có li độ x2 = –0,5 cm tương ứng với nửa chu kì thứ hai.
→ Tốc độ của vật tại vị trí vật đi được quãng đường S = 12 cm kể từ lúc thả.
v = ω A 2 2 − x 2 2 = 300 0 , 3 3 , 5 2 − 0 , 5 2 = 109 , 54 c m
Đáp án B
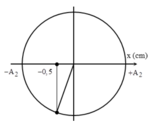

Đáp án C
+ Vật bắt đầu giảm tốc tại vị trí: x 0 = μ m g 2 k = 0,02m

Vị trí này được coi vị trí cân bằng ảo trong dao động tắt dần.
+ Năng lượng mất đi để chống lại lực ma sát. Vì vậy cơ năng mất tính bởi A = μ m g s = μ m g ( A - x 0 ) = 7,2 mJ

Đáp án D
Biên độ giảm trong khoảng thời gian T 2 là 1 cm
Vị trí cân bằng mới (l) lệch so với vị trí cân bằng cũ là 0,5 cm
Kéo giản thả => đi từ vị trí ban đầu đến 0 là 5 cm, đi một đoạn A 2 = 5 -1 = 4 cm nửa là còn 3 cm => đi vòng lại cái nửa 3 cm thì nó đủ 12 cm lúc này nó nằm tại M . M cách O một đoạn 1 cm, cách I một đoạn 0,5 cm; A 2 đúng là ( 4 – 0,5) cm
⇒ v = ω 3 , 5 2 - 0 , 5 2 = 109 , 5455 c m / s = 1 , 095 m / s

Đáp án D
Trong dao động tắt dần, độ lệch VTCB là Δ l = μ m g k = 0 , 5 ( c m )
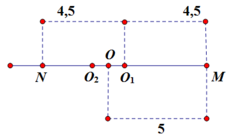
Ban đầu vật ở vị trí M, khi thả vật thì VTCB mới sẽ là O1, biên độ mới A’ = 4,5 cm, vật đi 1 đoạn MN = 9cm. Lúc này vật quay lại VTCB mới O2 với biên độ A ' ’ ’ = 3 , 5 c m .
Theo đề bài, ta phải tìm tốc độ của vật khi vật đi được tổng là 12cm. Lúc này vật đi được 9cm rồi nên cần đi thêm 3cm nữa, tức là tại thời điểm cần tìm tốc độ, vật cách VTCB O2 0,5 cm = > x = 0 , 5 c m . Công thức v = ω A 2 − x 2 = 1 , 095 ( m / s )

Hướng dẫn: Chọn đáp án C
Cách 1: Độ giảm cơ năng đúng bằng công của lực ma sát:

![]()
Cách 2: Xem I là tâm dao động và biên độ A 1 = A - x 1 , tốc độ tại O:
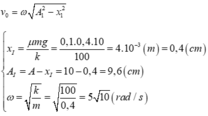
![]()
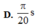


Bản chất của dao động này, khi xét chuyển động của vật từ biên trái sang phải thì có thể coi nó là điều hòa với VTCB mới lệch sang trái 1 đoạn x0.
Còn chuyển động của vật từ biên phải sang trái thì ngược lại. x0 đc xác định tại vị trí lực đàn hồi cân bằng với lực ma sát.
Ta có: \(kx_0=\mu mg\Rightarrow x_0=\frac{\mu mg}{k}=\frac{0,1.0,2.10}{10}=0,02m=2cm\)
Lực đàn hồi của lò xo nhỏ nhất ở VTCB.
Ta cần tìm thời gian vật đi từ x = 6cm về VTCB. Xét trên nửa dao động này, ta coi cđ của vật là điều hòa nên áp dụng véc tơ quay như sau.
x O 6 2 120 VT Cân bằng mới
Từ đó, thời gian dao động là: \(\frac{120}{360}T=\frac{T}{3}=\frac{1}{3}.2\pi\sqrt{\frac{0,2}{10}}=0,296s\)
Đáp án D.