Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi AB là quãng đường con thuyền đi và AC là chiều rộng con sông
Quãng đường AB là: \(3.\dfrac{1}{30}=\dfrac{1}{10}\left(km\right)\)
Chiều rộng bờ sông AC là :\(_{\sin B=\dfrac{AC}{AB}\Leftrightarrow AC=AB.\sin B=\dfrac{1}{10}\sin60^o}\) =\(\dfrac{\sqrt{3}}{20}\)(km)
Vậy chiều rộng con sông là \(\dfrac{\sqrt{3}}{20}\) km

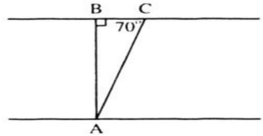
Kí hiệu như hình vẽ, trong đó:
AB là chiều rộng của khúc sông (cũng chính là đường đi của thuyền khi không có nước chảy).
AC là đoạn đường đi của chiếc thuyền (do nước chảy nên thuyền bị lệch).
Theo đề bài: v = 2km/h ; t = 5 phút = 1/12 h
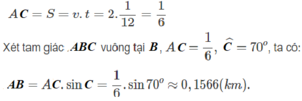
Vậy chiều rộng khúc sông là 0,1566 km = 156,6 m.

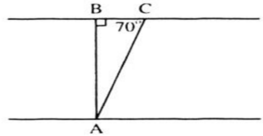
Kí hiệu như hình vẽ, trong đó:
AB là chiều rộng của khúc sông (cũng chính là đường đi của thuyền khi không có nước chảy).
AC là đoạn đường đi của chiếc thuyền (do nước chảy nên thuyền bị lệch).
Theo đề bài: v = 2km/h ; t = 5 phút = 1/12 h
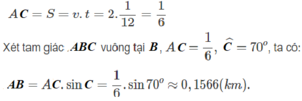
Vậy chiều rộng khúc sông là 0,1566 km = 156,6 m.

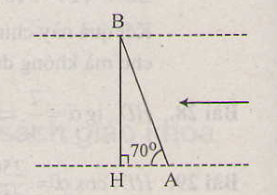
Gọi AB là đoạn đường mà con thuyền đi được trong 5 phút, BH là chiều rộng của khúc sông.
Xét tam giác ABH vuông tại H, biết cạnh huyền AB và một góc nhọn thì có thể tính được BH.
Quãng đường thuyền đi trong 5 phút =112h=112h là:
AB=2⋅112=16(km)AB=2⋅112=16(km)
Chiều rộng khúc sông là: BH=AB⋅sinA=16sin70∘≈0,1566(km)≈157(m)BH=AB⋅sinA=16sin70∘≈0,1566(km)≈157(m).
Độ dài AB là \(4\cdot\dfrac{1}{6}=\dfrac{2}{3}\left(km\right)\)
Chiều dài AH là \(\sin60^0\cdot AB=\dfrac{\sqrt{3}}{2}\cdot\dfrac{2}{3}=\dfrac{\sqrt{3}}{3}\left(km\right)\)
sao lại sin60 phải là cos60 chứ