Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Chu kì dao động
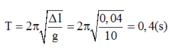
Trong một chu kì dao động, thời gian lò xo bị nén là khoảng thời gian vật đi từ x = ∆l đến x = A rồi trở về x = ∆l, tức là ∆t = 2t0 với t0 là thời gian đi từ x = ∆l đến x = A (giả sử chiều dương của trục tọa độ hướng lên).
Theo giả thiết:
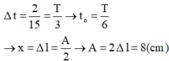
Khi lò xo giãn 8 cm 
vật đang chuyển động chậm dần đều nên đang đi ra biên, đi theo chiều dương hướng xuống
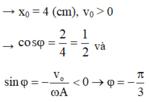
Đáp án B
Vận tốc có độ lớn cực đại là 0,4m/s nên 
Lúc vật đang ở vị trí x=2(cm) theo chiều dương thì tại đó động năng bằng ba lần thế năng nên:
W đ = 3 W t ⇒ 4 W t = W ⇒ 4 kx 2 2 = kA 2 2 ⇒ A = 2 x = 4 cm .
Gốc thời gian tại lúc này nên
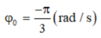
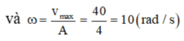
Vậy phương trình dao động của vật là:
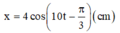
+ ω = g Δ l = 5 10 = 5 π
+ Khi lò xo giãn 8 cm thì x 0 = Δ l = 4 cm
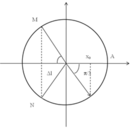
+ Thời gian lò xo bị nén tương ứng khi vật đi từ M đến N trên giản đồ.
φ n = t n . ω = 2 15 .5 π = 2 π 3
+ Vì N và M đối xứng nhau nên φ 0 = π 3 và mang dấu âm vì đang chuyển động chậm dần theo chiều dương (đang đi về biên dương)
Đáp án C
Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)
Đáp án C
Phương pháp: Sử dụng lí thuyết về phương trình dao động điều hòa
Cách giải :
Vị trí cân bằng lò xo dãn một đoạn ∆ ε , ta có:
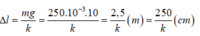
Vật được thả nhẹ từ vị trí lò xo dãn 6,5cm => biên độ dao động: A = 6,5 - 250 k
Vì A < 6,5cm nên dựa vào đáp án ta chọn A = 4cm
=> Phương trình dao động của vật: x = 4cos(20t) (cm)
Chọn đáp án C
Thế năng gấp 3 lần động năng khi:
x = A 3 2 .
Khoảng thời gian ngắn nhất giữa 2 lần khi vật đi quanh biên.
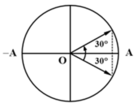
Từ hình vẽ:
1 12 s = T 6 ⇒ T = 0 , 5 s ⇒ ω = 4 π r a d / s .
Ta có:
7 4 s = 3 , 5 T ⇒ S = 14 A ⇒ A = 4 c m .
Vậy x = 4cos(4 π t - π /2) cm.
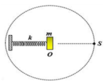
- S chuyển động tròn đều trên đường tròn tâm O bán kính 5cm với tốc độ góc 10π (rad/s)
- Vật m dao động điều hoà với với:
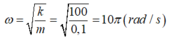
Tốc độ cực đại của m là : vmax = ωA = 50π cm/s => A = 5cm.
- Tại thời điểm nào đó, điểm sáng S đang đi qua vị trí như trên hình vẽ, còn vật nhỏ m đang có tốc độ cực đại (m có tốc độ cực đại khi qua vị trí cân bằng) => S và m luôn lệch pha nhau góc π/2.
S và m cách nhau lớn nhất khi m và S đi xung quanh vị trí cân bằng. Biểu diễn trên đường tròn lượng giác ta có :
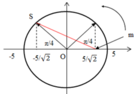
Áp dụng định lí Py – ta – go, ta có khoảng cách lớn nhất giữa S và m (đường màu đỏ) là :
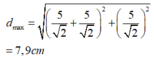
Đáp án D
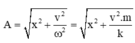
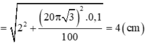
Gọi \(l\) là chiều dài lò xo lúc ko biến dạng \(\Rightarrow\left\{{}\begin{matrix}l_{max}=l+A=30\\l_{min}=l-A=20\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}l=25cm\\A=5cm\end{matrix}\right.\)
Khi lò xo dài 30cm, tức là vật đang ở biên dương, độ lớn của gia tốc là 8m/s^2\(\Rightarrow\left|a\right|=\omega^2A=800\left(cm/s^2\right)\Leftrightarrow\omega=\sqrt{\dfrac{800}{A}}=\sqrt{\dfrac{800}{5}}=4\pi\left(rad/s\right)\)
Gốc thời gian là lúc vật qua O theo chiều âm, tức là pha ban đầu bằng pi/2
\(\Rightarrow x=5\cos\left(4\pi t+\dfrac{\pi}{2}\right)\left(cm\right)\)
b/ \(W_d=3W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{3+1}}=\pm\dfrac{A}{2}\)
Nghĩa là khi vật qua vị trí có li độ là \(\left[{}\begin{matrix}x=-2,5cm\\x=2,5cm\end{matrix}\right.\)
c/ Góc vật quay được trong thời gian delta t là: \(\varphi=\omega.\Delta t=4\pi.\Delta t\left(rad\right)\)
Quãng đường lớn nhất đi được khi vật chuyển động xung quanh vtcb
\(S_{max}=2A.\sin\left(2\pi.\Delta t\right)\)
Quãng đường nhỏ nhất đi được khi vật chuyển động xung quang biên
\(S_{min}=2A-2.A\cos\left(2\pi.\Delta t\right)\)
\(\Rightarrow S_{max}-S_{min}=2A\left(\sin\left(2\pi.\Delta t\right)-1+\cos\left(2\pi.\Delta t\right)\right)\)
Xét \(M=\sin\left(2\pi.\Delta t\right)+\cos\left(2\pi.\Delta t\right)=\cos\left(2\pi\Delta t-\dfrac{\pi}{2}\right)+\cos\left(2\pi\Delta t\right)=2\cos\left(\dfrac{2\pi\Delta t-\dfrac{\pi}{2}+2\pi\Delta t}{2}\right)\cos\left(\dfrac{2\pi\Delta t-\dfrac{\pi}{2}-2\pi\Delta t}{2}\right)\)
\(M=2\cos\left(2\pi\Delta t-\dfrac{\pi}{4}\right)\cos\left(\dfrac{\pi}{4}\right)\)
Để \(\left(S_{max}-S_{min}\right)_{max}\Leftrightarrow M_{max}\Leftrightarrow\cos\left(2\pi\Delta t-\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow2\pi\Delta t-\dfrac{\pi}{4}=0\Leftrightarrow\Delta t=\dfrac{\pi}{4.2\pi}=\dfrac{1}{8}\left(s\right)\)
d/ Ta thấy vật N luôn dao động vuông pha với vật M
\(\Rightarrow\left(\dfrac{x_M}{A_M}\right)^2+\left(\dfrac{x_N}{A_N}\right)^2=1\Leftrightarrow\left(\dfrac{2,5\sqrt{3}}{5}\right)^2+\left(\dfrac{x_N}{10}\right)^2=1\Leftrightarrow x_N=\pm2,5\left(cm\right)\)
Tính khoảng cách nên ko cần quan tâm xN dương hay âm
\(MN=\sqrt{ON^2+OM^2}=\sqrt{2,5^2+\left(2,5\sqrt{3}\right)^2}=5cm\)
em cảm ơn ạ