Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Biên độ: \(A=10cm\)
Tần số góc: \(\omega=10(rad/s)\)
Tại vị trí lò xo bị giãn \(5cm\) thì li độ của vật là: \(x=-10+5=-5cm\)
Vật đang đi lên là chuyển động theo chiều âm.
\(\Rightarrow \cos\varphi=-\dfrac{5}{10}=-0,5\)
\(\Rightarrow \varphi = \dfrac{2\pi}{3}\) (rad) (vì vật chuyển động theo chiều âm nên \(\varphi < 0\) )
PT dao động: \(x=10\cos(10t+\dfrac{2\pi}{3}) (cm)\)
Ở VTCB lò xo giãn 10 cm, như vậy để nó giãn 5cm thì từ VTCB phải đi lên 5cm.
Chiều dương hướng xuống, nên li độ lúc đó phải bằng -5cm.
O -5cm -10cm Lò xo không biến dạng Lò xo giãn 5cm Lò xo giãn 10cm x

Do \(\alpha_0=8^0\) nên đây là dao động điều hòa, ta tính toán giống như một dao động điều hòa thôi.
Tại vị trí \(W_đ=W_t\)
\(\Rightarrow W=W_đ+W_t=2W_đ\)
\(\Rightarrow v_{max}^2=2.v^2\)
\(\Rightarrow v=\dfrac{v_{max}}{\sqrt 2}=\dfrac{\omega.A}{\sqrt 2}\)
\(\Rightarrow v=\dfrac{\sqrt{\dfrac{g}{\ell}}.\alpha_0.\ell}{\sqrt 2}=\dfrac{\alpha_0.\sqrt{g.\ell}}{\sqrt 2}\)
\(\Rightarrow v=\dfrac{\dfrac{8.\pi}{180}.\sqrt{10.1}}{\sqrt 2}\approx0,31(m/s)\)

Chọn B
+Khi có lực lạ gia tốc trọng trường biểu kiến 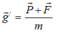
Trong trường hợp cụ thể:
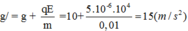
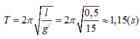

Chu kì dao động: T = 2π/ω = 2π/5π = 0,4s
Thời điểm t = 0 và thời điểm độ lớn lực đàn hồi bằng 0,5N được biểu diễn trên đường tròn lượng giác:
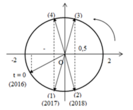
Một chu kì có 4 lần độ lớn lực đàn hồi bằng 0,5N
Sau 504T độ lớn lực đàn hồi bằng 0,5N lần thứ 2016
=> Lực đàn hồi có độ lớn bằng 0,5N lần thứ 2018 vào thời điểm:
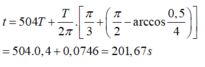
Đáp án C


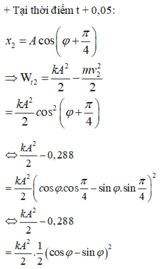


Thời gian lò xo giãn trong một chu kì được biểu diễn trên đường tròn lượng giác:

Đáp án D
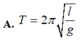
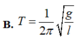
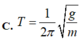

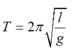

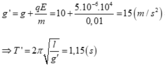
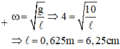
cho mk xin cả cách giải nha