Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

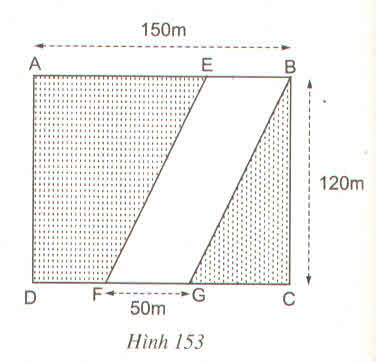
Con đường hình bình hành EBGF có diện tích
SEBGF = 50.120 = 6000 m2
Đám đất hình chữ nhật ABCD có diện tích
SABCD = 150.120 = 18000 m2
Diện tích phần còn lại của đám đất:
S = SABCD - SEBGF = 18000 – 6000 = 12000 m2

Con đường hình bình hành EBGF có diện tích
SEBGF = 50.120 = 6000 m2
Đám đất hình chữ nhật ABCD có diện tích
SABCD = 150.120 = 18000 m2
Diện tích phần còn lại của đám đất:
S = SABCD - SEBGF = 18000 – 6000 = 12000 m2

Con đường hình bình hành EBGF có diện tích:
SEBGF = 50.120 = 6000 (m2)
Đám đất hình chữ nhật ABCD có diện tích:
SABCD = 150.120 = 18000(m2)
Diện tích phần còn lại của đám đất:
S= SABCD - SEBGF = 18000 - 6000 = 12000(m2)
Con đường hình bình hành EBGF có diện tích:
SEBGF = 50.120 = 6000 (m2)
Đám đất hình chữ nhật ABCD có diện tích:
SABCD = 150.120 = 18000(m2)
Diện tích phần còn lại của đám đất:
S= SABCD - SEBGF = 18000 - 6000 = 12000(m2)

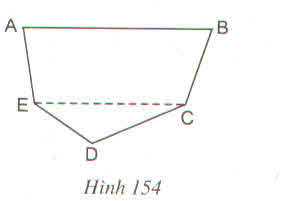
Chia đám đất ABCDE thành hình thang ABCE và tam giác ECD. Cần vẽ đường cao CH của hình thang và đường cao DK của tam giác. Thực hiện các phép đo chính xác đến mm ta được AB = 30mm, CE = 26mm, CH = 13mm, DK = 7mm.
Nên SABCE = \(\dfrac{\text{(AB+EC).CH}}{2}\) = \(\dfrac{\text{(30+26).13 }}{2}\)=364 (mm2)
SECD = \(\dfrac{1}{2}\) EC. DK = \(\dfrac{1}{2}\)267= 91 (mm2)
Do đó SABCDE = SABCE + SECD = 364 + 91 = 455 (mm2)
Vì bản đồ được vẽ với tỉ lệ xích \(\dfrac{1}{5000}\) nên diện tích đám đất là:
S = 455. 5000 = 2275000 (mm2) = 2,275 (m2)

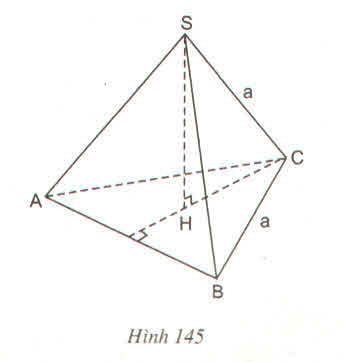
V = \(\dfrac{1}{3}\)S . h = \(\dfrac{1}{3}\)a.h.h = \(\dfrac{1}{3}\)ah2

Ta có hình thang ABCD ( AB// CD), với đường trung bình EF và hình chữ nhật GHIK như hình vẽ .
Dễ dàng chứng minh
∆AEG = ∆DEK;
∆BFH = ∆CFI
Do đó SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
Nên
SABCD = SGHIK = EF. AJ mà EF = EF=AB+CD2EF=AB+CD2
Do đó SABCD = SABCD=AB+CD2.AJSABCD=AB+CD2.AJ
Vậy ta gặp lại công thức tính diện tích hình thang đã được học nhưng bằng một phương pháp chứng minh khác. Mặt khác, ta phát hiện công thức mới : Diện tích hình thang bằng tích của đường trung bình hình thang với chiều cao.

Ta có hình thang ABCD ( AB// CD), với đường trung bình EF và hình chữ nhật GHIK như hình vẽ .
Dễ dàng chứng minh
∆AEG = ∆DEK;
∆BFH = ∆CFI
Do đó SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
Nên
SABCD = SGHIK = EF. AJ mà EF = EF=AB+CD2EF=AB+CD2
Do đó SABCD = SABCD=AB+CD2.AJSABCD=AB+CD2.AJ
Vậy ta gặp lại công thức tính diện tích hình thang đã được học nhưng bằng một phương pháp chứng minh khác. Mặt khác, ta phát hiện công thức mới : Diện tích hình thang bằng tích của đường trung bình hình thang với chiều cao.

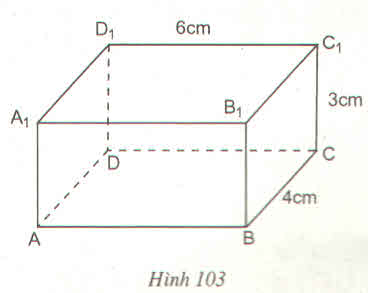
\(S_{XQ}=\left(4+6\right)\cdot2\cdot3=60\left(cm^2\right)\)
\(S_{TP}=60+24\cdot2=108\left(cm^2\right)\)

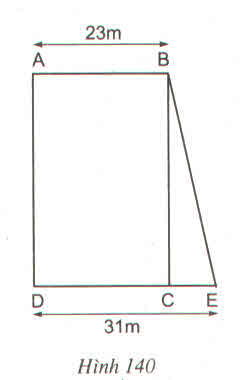
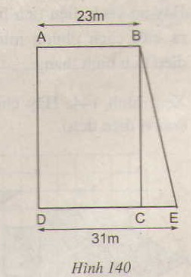
Ta có SABCD = AB. AD = 828 m2
Nêm AD = 8282382823 = 36 (m)
Do đó diện tích của hình thang ABED là:
SABED= (AB+DE).AD2(AB+DE).AD2 = (23+31).362(23+31).362 = 972(m2)
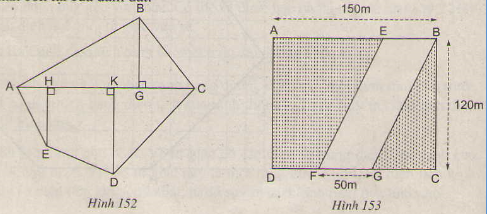



Con đường hình bình hành EBGF có diện tích:
SEBGF = 50.120 = 6000 (m2)
Đám đất hình chữ nhật ABCD có diện tích:
SABCD = 150.120 = 18000(m2)
Diện tích phần còn lại của đám đất:
S = SABCD - SEBGF = 18000 - 6000 = 12000(m2)
Đáp số: 6000 m2 và 12000 m2
Con đường hình bình hành EBGF có diện tích:
SEBGF = 50.120 = 6000 (m2)
Đám đất hình chữ nhật ABCD có diện tích:
SABCD = 150.120 = 18000(m2)
Diện tích phần còn lại của đám đất:
S= SABCD - SEBGF = 18000 - 6000 = 12000(m2)