Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi S(km) là quãng đường ô tô đó chuyển động.
Ta có: Vận tốc trung bình của người đó là: Vtb = \(\dfrac{S_1+S_2+S_3}{t_1+t_2+t_3}\) = \(\dfrac{S}{t_1+t'}\)(km/h) (1)
mà t1 = \(\dfrac{S_1}{v_1}\) = \(\dfrac{S}{2v_1}\) = \(\dfrac{S}{120}\)(h) (2)
Ta lại có: S2 + S3 = \(\dfrac{S}{2}\)
⇔V2.t2 + V3.t3 = \(\dfrac{S}{2}\)
⇔\(\dfrac{V_2.t'}{2}\) + \(\dfrac{V_3.t'}{2}\) = \(\dfrac{S}{2}\)
⇔V2.t' + V3.t' = S
⇔15t' + 46t' = S
Cre: Netflix
⇔61t' = S
⇒t' = \(\dfrac{S}{61}\)(h) (3)
Thay (2) và (3) vào (1) ta được:
Vtb = \(\dfrac{S}{\dfrac{S}{120}+\dfrac{S}{61}}\) = \(\dfrac{S}{S\left(\dfrac{1}{120}+\dfrac{1}{61}\right)}\) = \(\dfrac{1}{\dfrac{1}{120}+\dfrac{1}{61}}\) = 40,442(km/h).

Giải thích: Đáp án D
Phương pháp :
- Áp dụng định luật bảo toàn động lượng và định luật bảo toàn động năng
- Sử dung̣ hê ̣thức đôc̣ lâp̣ với thời gian của li đô ̣vàvâṇ tốc
Biên độ dao động ban đầu: ![]()
Cách giải:
Hai vật va chạm đàn hồi xuyên tâm nên áp dụng ĐL bảo toàn động lượng và động năng ta được:
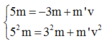
Giải hệ ta được v = 2cm/s
Áp dụng hệ thức độ lập: 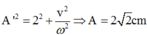
Vậy quãng đường đi được sau va chạm đến khi đổi chiều chuyển động là

Ta có:\(\begin{cases} A^2=\dfrac{v_{0}^2}{\omega^2} \\ A^2=x^2+\dfrac{v_{0}^2}{4\omega^2} \end{cases}\)
\( \Rightarrow x=\dfrac{\sqrt{3}A}{2}\)
Góc quét \(\dfrac{\pi}{3}=\dfrac{2.\pi}{T}.\dfrac{\pi}{15} \Rightarrow T=\dfrac{2\pi}{5}\)
Ta có: \( \dfrac{3\pi}{10}=\dfrac{\pi}{5}+\dfrac{\pi}{10}=\dfrac{T}{2}+\dfrac{\pi}{10}\)
Nên vật đi được quãng đường \(3A=12 \Rightarrow A=4 \Rightarrow v_{0}=20\)

a) 20 phút = 1/3 h
24 phút = 2/5 h
Độ dài quãng đường đầu đi được là :
s1 = v1 . t1 = 15 . 1/3 = 5 km
Độ dài quãng đường còn lại là :
s2 = v2 . t2 = 18 . 2/5 = 7,2 km
Độ dài quãng đường AB là :
s = s1 + s2 = 5 + 7,2 = 12,2 km
b) Vận tốc trung bình của người đó trên quãng đường AB là :
\(V_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{12,2}{\dfrac{1}{3}+\dfrac{2}{5}}=16\dfrac{7}{11}\)km/h



Tóm tắt:
\(2s=360m\)
\(v_1=5\)m/s
\(v_2=4\)m/s
--------------
\(t_{AB}=?\)
\(v_{tb}=?\)
Giải:
Thời gian đi hết nửa đoạn đường đầu là:
\(v_1=\dfrac{s}{t_1}\Rightarrow t_1=\dfrac{s}{v_1}=\dfrac{360:2}{5}=36\left(s\right)\)
Thời gian đi hết nửa đoạn đường sau là:
\(v_2=\dfrac{s}{t_2}\Rightarrow t_2=\dfrac{s}{v_2}=\dfrac{360:2}{4}=45\left(s\right)\)
Thời gian vật đến B là:
\(t_{AB}=t_1+t_2=36+45=81\left(s\right)\)
Vận tốc trung bình là:
\(v_{tb}=\dfrac{s+s}{t_1+t_2}=\dfrac{360}{81}=\dfrac{40}{9}\)(m/s)
thời gian đi nữa đoạn đầu là
t1=\(\dfrac{s.0,5}{v_1}\)=36s
thời gian đi nữa đoạn sau là
t2=\(\dfrac{s.0,5}{v_2}\)=45s
sau 81s vật từ A đến B
vtb=\(\dfrac{s}{t_1+t_2}\)=\(\dfrac{40}{9}\)m/s