Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(v_{max} = A\omega\)
Dựng đường tròn ứng với vận tốc
0 Aω -Aω 20π -20π φ π/3 M Q P N a b H
Cung tròn ứng với tốc độ của vật không vượt quá \(20\pi (cm/s)\) là \(\stackrel\frown{QaM} = \varphi; \stackrel\frown{NbP}= \varphi\)
=> thời gian để tốc độ (độ lớn của vận tốc) không vượt quá \(20\pi (cm/s)\) là:
\(t = \frac{2\varphi}{\omega} \)
mà giả thiết: \(t = \frac{2T}{3}s\) => \(\frac{2\varphi}{\omega} = \frac{2T}{3}\)
=> \(\varphi = \frac{2T}{3}.\frac{\omega}{2}= \frac{2\pi}{3}\) (do \(\omega = \frac{2\pi}{T}\))
=> \(\widehat{MOH} = \frac{\varphi}{2} = \frac{\pi}{3}\)
Ta có: \(\cos \widehat{MOH} =\frac{1}{2}= \frac{20\pi}{A\omega} \)
=> \(\omega = \frac{2.20\pi}{5} = 8\pi\)
=> \(T = \frac{2\pi}{\omega} =0,25s. \)
Vậy \(T= 0,25s.\)
cung tròn ko vượt quá 20pi thì là góc NOM và góc POQ chứ ??

Độ lớn của gia tốc không vượt quá 100 c m / s 2 là một phần 3 chu kì → 1 2 ω 2 A = 100 .
→ ω = 2 π rad / s → f = 1 Hz
Đáp án A

Đáp án C.
Xét
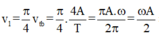
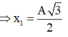
Vùng tốc độ ≥ v 1 nằm trong - x 1 ; x 1
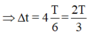 kết hợp với bài ta có T=0,5(s)
kết hợp với bài ta có T=0,5(s)
Phân tích 1 6 = T 3 quãng đường lớn nhất vật đi được trong T 3 khi vật đi qua lân cận vị trí cân bằng
Công thức
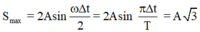 ,
,
đối chiếu với giả thiết ta có A=2(cm)
Vận tốc cực đại của vật trong quá trình chuyển động
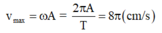
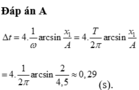

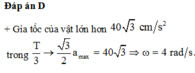

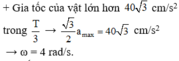
\(\omega=2\pi/T=8\pi(rad/s)\)
Tốc độ cực đại của vật là: \(v_{max}=\omega.A=8\pi.5=40\pi(cm/s)\)
Ta biểu diễn biến thiên của vận tốc bằng véc tơ quay:
40π -40π > v 20π 60° M N P Q
Để \(|v|\ge 20\pi\) thì ứng với véc tơ quay từ M đến N và P đến Q.
Góc quay:
\(\alpha=4.60=240^0\)
Thời gian: \(t=\dfrac{240}{360}T=\dfrac{2}{3}.0,25=\dfrac{5}{30}s\)