Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vận tốc tại vị trí cân bằng:
vmax=A.w=40(cm/s) (1)
gia tốc tại vị trí biên:
a(max)=A.w^2=200(cm/s^2) (2)
lập tỉ số (2)/(1) ta được:
w=5(rad/s)
thế w vào (1)=>A=8(cm) = 0,8 m

+ Khi qua VTCB, vận tốc cực đại, nên: vmax=20 cm/s.
+ Do: \(a = v'_{(t)} \Rightarrow (v_{max})^2 = v^2+(\frac{a}{\omega})^2 \Rightarrow (20)^2 = 10^2+(\frac{40\sqrt 3}{\omega})^2 \Rightarrow \omega = 4\ (rad/s)\)
+ Biên độ: \(A = \frac{v_{max}}{\omega}=\frac{20}{4} = 5 \ (cm)\)

Đáp án D
+ Tốc độ của vật khi đi qua vị trí cân bằng v = v max = ωA = 20 cm/s.→ Gia tốc và vận tốc trong dao động điều hòa là vuông pha nhau, ta có công thức độc lập thời gian
v ωA 2 + a ω 2 A 2 = 1 ⇔ 10 20 2 + 40 3 20 ω 2 = 1

Tốc độ của vật khi đi qua vị trí cân bằng
![]()
Gia tốc và vận tốc trong dao động điều hòa là vuông pha nhau, ta có công thức độc lập thời gian
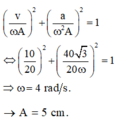
Đáp án D



Ta có:
\(\left\{{}\begin{matrix}\omega A=20\pi\\\omega^2A=40\pi^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\omega=2\pi\left(rad\text{/}s\right)\\A=10\left(cm\right)\end{matrix}\right.\)
\(t=0\left\{{}\begin{matrix}\cos\varphi=\dfrac{x}{A}=-\dfrac{1}{2}\\v>0\Rightarrow sin\varphi< 0\end{matrix}\right.\Rightarrow\varphi=-\dfrac{2\pi}{3}\)
Vậy phương trình dao động là: \(x=10\cos\left(2\pi t-\dfrac{2\pi}{3}\right)cm\)