Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

 |
Đề bài: tính diện tích phần bôi đen (đơn vị cm)
Đáp án: Lấy diện tích hình chữ nhật trừ đi diện tích hai hình tròn rồi chia đôi. Sau đó bôi đen góc nhọn phía dưới bên trái.
 |
Điều cần làm là tính diện tích hình màu đỏ và nó được tính như sau:
1. Diện tích góc màu xanh = (Diện tích hình vuông 10*10 - diện tích hình tròn) chia cho 4
2. Diện tích cung màu vàng = diện tích cung hình tròn - diện tích tam giác ABD
- Diện tích tam giác ABD khá đơn giản khi biết cạnh AB = 5 và góc ACB có tang = 1/2.
- Trong đó diện tích cung tròn cũng dễ dàng tìm ra khi biết được góc của cung là (180-2*góc CAB).
3. Vậy diện tích phần màu đỏ = Diện tích tam giác LAM - diện tích cung màu vàng - diện tích góc màu xanh.

chiều dài là : 11 m
chiều rộng là : 7 m

a, Tính lượng nước \(\left(m^3\right)\)anh Minh đổ vào hố sau mỗi làn gánh ( ghi kết quả làm tròn đến 2 chữ số thập phân )
Biết trong quá trình gánh nước thì lượng nước bị hao hụt khoảng 10% nên
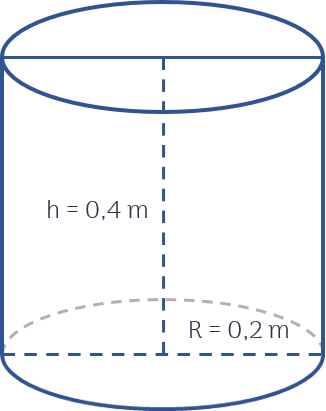
Công thức tính thể tích hình trụ là : \(V=ttR^2h\)
Thể tích của 2 thùng nước mỗi lần anh Minh gánh được là :
\(V_1=2ttR^2h=2tt\times0,0^2\times0,4=0,032tt\left(m^3\right)\)
Trong quá trình gánh , lượng nước hao hụt 10% nên lượng nước thực tế anh Minh đổ vào hồ sau mỗi lần gánh là :
\(V=0,032tt\times90\%=0,09\left(m^3\right)\)
b, Thể tích của hồ nước hình chữ nhật là :
\(V_0=2\times2\times1=4\left(m^3\right)\)
Số lần ít nhất anh Minh cần gánh để đổ đầy hồ nước là :
\(n=[\frac{V_0}{V}]+1=[\frac{4}{0,09}]+1=44+1=45\)Lần