Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kí hiệu Ak: “ lần thứ k lấy được con át” k≥1 thì P(A1)=4/52=1/13
b. ta cần tính :
![]()
Chọn C

Kí hiệu \(A_k:\)" Lần thứ k lấy được con át", \(k\ge1\). Rõ ràng \(A_1,A_2\) độc lập
a) Ta cần tính \(P\left(\overline{A_1}\cap A_2\right)\). Ta có \(P\left(\overline{A_1}\cap A_2\right)=P\left(\overline{A_1}\right)P\left(A_2\right)=\dfrac{48}{52}.\dfrac{4}{52}\)
b) Theo bài ra ta cần tính :
\(P\left(A_1\right)+P\left(\overline{A_1}\cap A_2\right)=\dfrac{4}{52}+\dfrac{48}{52}.\dfrac{4}{52}\approx0,15\)

Kí hiệu A k : Lần thứ k lấy được con át , k ≥ 1 . Rõ ràng A 1 , A 2 độc lập.
a) Ta cần tính P ( A 1 ∩ A 2 ) .
Ta có:
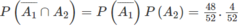
b) Theo bài ra ta cần tính:
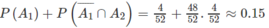

Phép thử T được xét là: "Từ cỗ bài tú lơ khơ 52 con bài, rút ngẫu nhiên 4 con bài".
Mỗi kết quả có thể có là một tổ hợp chập 4 của 52 con bài. Do đó số các kết quả có thể có của phép thử T là n(Ω) = C452 = = 270725.
Vì rút ngẫu nhiên nên các kết quả có thể có là đồng khả năng.
a) Gọi biến cố A: "Rút được bốn con át". Ta có, số kết quả có thể có thuận lợi cho A là n(A) = 1. Suy ra P(A) = ≈ 0,0000037.
b) Gọi biến cố B: "Rút được ít nhất một con át". Ta có
= "Rút được 4 con bài đều không là át". Mỗi kết quả có thể thuận lợi cho
là một tổ hợp chập 4 của 48 con bài không phải là át. Suy ra số các kết quả có thể có thuận lợi cho
là C448 =
= 194580. Suy ra P(
) =
≈ 0,7187.
Qua trên ta có P(B) = 1 - P() ≈ 0,2813.
c) Gọi C là biến cố: "Rút được hai con át và hai con K".
Mỗi kết quả có thể có thuận lợi cho C là một tổ hợp gồm 2 con át và 2 con K. Vận dụng quy tắc nhân tính được số các kết quả có thể có thuận lợi cho C là
n(C) = C24 C24 = 6 . 6 = 36.
Suy ra P(C) = ≈ 0,000133.

Không gian mẫu là kết quả của việc chọn ngẫu nhiên 4 con trong số 52 con
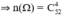
a. Đặt A : « Cả 4 con lấy ra đều là át »
⇒ n(A) = 1
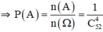
b. + B : « Không có con át nào trong 4 con khi lấy ra »
⇒ B là kết quả của việc chọn ngẫu nhiên 4 con trong số 48 con còn lại
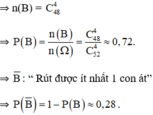
c. C: “Rút được 2 con át và 2 con K”.
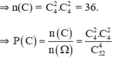

Số cách rút ra 13 con bài là : \(C_{52}^{13}\). Như vậy \(n\left(\Omega\right)=C_{52}^{13}\)
Kí hiệu A : " Trong 13 con bài có 4 con pích, 3 con rô, 3 con cơ và 3 con nhép"
Ta có :
\(n\left(A\right)=C_{13}^4.C_9^3.C_6^3=\dfrac{13!}{4!\left(3!\right)^3}\)
Vậy :
\(P\left(A\right)=\dfrac{13!}{4!\left(3!\right)^3.C^{13}_{52}}\approx0,000002\)

Số cách rút ra 13 con bài là 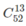 . Như vậy n(Ω) =
. Như vậy n(Ω) = 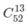
Kí hiệuA : "Trong 13 con bài có 4 con pích, 3 con rô, 3 con cơ và 3 con nhép".
Ta có 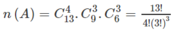
Vậy 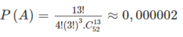

Lời giải:
Lấy 3 quân ngẫu nhiên từ 52 quân có $C^3_{52}$ cách
a. Lấy được 3 quân át, có $C^3_4=4$ cách
Xác suất: $\frac{4}{C^3_{52}}=\frac{1}{5525}$
b. Lấy được 1 quân át, 2 quân còn lại khác, có $C^1_4.C^2_{48}$ cách
Xác suất: $\frac{C^1_4.C^2_{48}}{C^3_{52}}=\frac{1128}{5525}$
c.Lấy được 2 quân cơ, 1 quân bất kỳ, có:
$C^2_4.C^1_{48}$
Xác suất: $\frac{C^2_4.C^1_{48}}{C^3_{52}}=\frac{72}{5525}$


Kí hiệu Ak: “ lần thứ k lấy được con át” k≥1 thì P(A1)=4/52=1/13
a. Ta tính P(A1)= 1/13
Chọn B