
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Rút ra một lá bài gồm 52 lá .Xác suất để rút được 2 lá chất cơ là
Giải giúp mình với ạ .Mình cảm ơn.

-n(Ω)= 52
-n(A): 13C2 (1 bộ bài 52 lá có 13 lá chất cơ, rút ra 2 lá)
-P(A): 13C2 /52 = 3/2
ko biết đúgn ko lâu r ko làm +))

Để có tổng bằng 21,ta có thể làm như sau:
Ta rút :
C1: 10 và J *Vì hai lá này có giá trị là:10,11*
C2: 9 và Q *GIÁ trị 9 và 12*
C3: 8 và K *giá trị 8 và 13*
Vậy có tổng cộng 3 cách rút được 2 lá có tổng bằng 21.

Không gian mẫu: \(365.365=365^2\)
Người thứ nhất có 365 khả năng ngày sinh, người thứ 2 chỉ có 1 khả năng trùng với người thứ nhất nên có \(365.1=365\) khả năng 2 người trùng ngày sinh
Xác suất: \(P=\dfrac{365}{365^2}=\dfrac{1}{365}\)

a: n(A)=2
n(omega)=2*2*2=8
=>P(A)=2/8=1/4
b: B={(NSS); (SNS); (SSN)}
=>n(B)=3
=>P(B)=3/8
c: C={NSS; NSN; SSN; SSS}
=>n(C)=4
=>P(C)=4/8=1/2
d: D={NSN; NNS; NNN; SNN; NSS; SNS; SSN}
=>n(D)=6
=>P(D)=6/8=3/4

a) Kí hiệu S là đồng xu ra mặt sấp và N là đồng xu ra mặt ngửa. Ta có sơ đồ cây
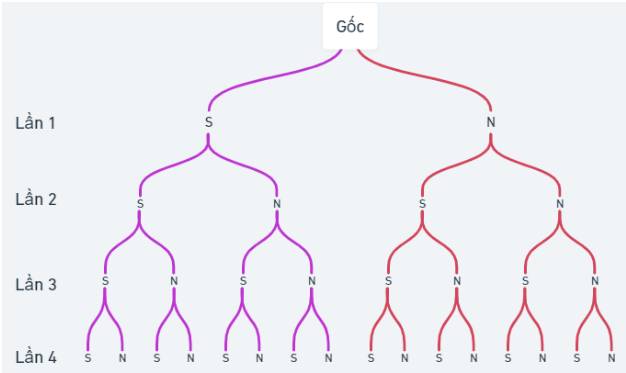
Dựa vào sơ đồ cây ta suy ra \(n\left( \Omega \right) = 16\).
b) Gọi A là biến cố: “gieo đồng xu 4 lần có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa”
Suy ra \(A = \left\{ {SSNN;SNSN;SNNS;NSSN;NSNS;NNSS} \right\}\). Suy ra \(n\left( A \right) = 6\). Vậy\(P\left( A \right) = \frac{6}{{16}} = \frac{3}{8}\).

Ta có : \(\overline{A}=\overline{A_1UA_2UA_3}=\overline{A_1}\) \(\overline{A_2}\)\(\overline{A_3}\)= sự kiện không có ai bắn trúng
\(\Rightarrow P\left(\overline{A}\right)=\)\((\overline{A_1}\)\(\overline{A_2}\)\(\overline{A_3})\)\(=P\left(\overline{A_1}\right)P\left(\overline{A_2}\right)P\left(\overline{A_3}\right)=0,5.0,4.0,3=0,06\)
\(\Rightarrow P\left(A\right)=1-P\left(\overline{A}\right)=1-0,06=0,94\)
Vậy xác xuất để con thú bị bắn trúng là 0,94

Có thể là 2 lần chẵn 1 lần lẻ hoặc cả 3 lần đều chẵn
TH1: 2 chẵn, 1 lẻ
=>Có \(C^1_3\cdot C^1_3\cdot C^1_3=27\left(cách\right)\)
TH2: 3 lần đều chẵn
=>Có \(C^1_3\cdot C^1_3\cdot C^1_3=27\left(cách\right)\)
=>Có 27+27=54 cách
n(omega)=6*6*6=216
=>P=54/216=1/4

+) Không gian mẫu của phép thử là: \(\Omega {\rm{ }} = {\rm{ }}\left\{ {SS;{\rm{ }}SN;{\rm{ }}NS;{\rm{ }}NN} \right\}.\) Vậy \(n\left( \Omega \right) = 4\)
+) Các kết quả thuận lợi cho biến cố A là: \(A{\rm{ }} = {\rm{ }}\left\{ {SS;{\rm{ }}NN} \right\}\). Vậy \(n\left( A \right) = 2\)
+) Xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{2}{4} = \frac{1}{2}\)

Gọi F là biến cố “ít nhất một con xúc xắc xuất hiện mặt 6 chấm”.
Biến cố \(\overline F \) là “ Cả hai con xúc xắc đều không xuất hiện mặt 6 chấm”.
Ta có \(n\left( \Omega \right) = 36\) và \(\overline F = \left\{ {\left( {i;j} \right),1 \le i;j \le 5} \right\}\) do đó \(n\left( {\overline F } \right) = 25\).
Vậy \(P\left( {\overline F } \right) = \frac{{25}}{{36}}\) nên \(P\left( F \right) = 1 - \frac{{25}}{{36}} = \frac{{11}}{{36}}\).
Không gian mẫu: \(\dfrac{52!}{\left(4!\right)^{13}}\)
Do đó xác suất: \(P=\dfrac{1}{\dfrac{52!}{\left(4!\right)^{13}}}=\dfrac{\left(4!\right)^{13}}{52!}=...\)
1.
ĐKXĐ: \(-3\le x\le1\)
\(2\left(x+3\right)-m\sqrt{x+3}+5\left(1-x\right)+2m\sqrt{1-x}=4\sqrt{\left(x+3\right)\left(1-x\right)}\)
\(\Leftrightarrow m\left(2\sqrt{1-x}-\sqrt{x+3}\right)=3x-11+4\sqrt{\left(x+3\right)\left(1-x\right)}\)
Đặt \(2\sqrt{1-x}-\sqrt{x+3}=t\Rightarrow t\in\left[-2;4\right]\)
\(t^2=7-3x-4\sqrt{\left(1-x\right)\left(x+3\right)}\)
\(\Rightarrow3x-11+4\sqrt{\left(1-x\right)\left(x+3\right)}=-4-t^2\)
Do đó pt trở thành: \(m.t=-t^2-4\)
- Với \(t=0\) ko phải nghiệm
- Với \(t\ne0\Rightarrow m=\dfrac{-t^2-4}{t}\)
Xét \(f\left(t\right)=\dfrac{-t^2-4}{t}\) với \(t\in\left[-2;4\right]\)
\(f^2\left(t\right)=\dfrac{\left(t^2+4\right)^2}{t^2}\ge4\Rightarrow\left[{}\begin{matrix}f\left(t\right)\le-2\\f\left(t\right)\ge2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m\le-2\\m\ge2\end{matrix}\right.\)