Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Số phần tử của không gian mẫu:
![]()
Gọi A là biến cố “nhóm được chọn có cả nam và nữ, đồng thời mỗi khối có 1 học sinh nam”
⇒ số phần tử của biến cố A là: ![]()
![]() .
.

a.
Chọn 1 nam từ 9 nam có 9 cách
Chọn 1 nữ từ 3 nữ có 3 cách
\(\Rightarrow\) Có \(9.3=27\) cách chọn nhóm 1 nam 1 nữ
b.
Chọn 2 nhà toán học từ 8 nahf toán học: \(C_8^2\) cách
Chọn 2 nhà vật lý từ 4 nhà vật lý: \(C_4^2\) cách
\(\Rightarrow C_8^2.C_4^2\) cách lập
c.
Các trường hợp thỏa mãn: (1 nhà toán học nữ, 2 nhà vật lý nam), (1 nhà toán học nữ, 1 nhà toán học nam, 1 nhà vật lý nam), (2 nhà toán học nữ, 1 nhà vật lý nam)
\(\Rightarrow C_3^1.C_4^2+C_3^1.C_5^1.C_4^1+C_3^2.C_4^1\) cách

Đáp án D
Mỗi cách chọn là một tổ hợp chập 5 của 15 nên ![]()
Số cách chọn là
![]()
Xác suất cần tìm là: ![]()

Đáp án B
Phương pháp: Công thức tính xác suất của biến cố A là: P ( A ) = n A n Ω
Cách giải:
Chọn 3 đoàn viên trong 25 đoàn viên nên n Ω = C 25 3 = 2300
Gọi biến cố A: “Chọn 3 đoàn viên trong đó có 2 nam và 1 nữ”.
Khi đó ta có: n A = C 25 1 . C 10 2 = 675
Vậy xác suất cần tìm là:


Chọn 3 đoàn viên trong 25 đoàn viên thì có C253 cách chọn, do đó ta có: n(Ω) = C253 = 2300 phần tử
Có 10 đoàn viên nam chọn 2 đoàn viên thì có C102 cách chọn; có 15 đoàn viên nữ chọn 1 nữ thì có C151 cách chọn.
Gọi A là biến cố:”3 đoàn viên được chọn có 2 nam và 1 nữ” thì số phần tử của tập A là n(A) =C102.C151=675
Vậy P(A) =(n(A))/(n(Ω))=675/2300=27/92. Chọn đáp án B
Nhận xét: học sinh thường mắc một số sai lầm khi tính:
n(A) =C102+C151=60 ⇒P(A)=3/115
n(A) = A102.A151=1350;n(Ω)=A253=13800 ⇒ P(A)=9/92
n(A) = A102+A151=105;n(Ω)=A253=13800 ⇒P(A)=7/920
Chọn D





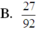
a. Chọn 3 người bất kì từ 100 người, có \(C_{100}^3\) cách
b. Chọn 2 nam từ 60 nam và 1 nữ từ 40 nữ, có \(C_{60}^2.C_{40}^1\) cách
c. Do anh A và chị B không đi nên chỉ chọn 3 người từ 98 người còn lại, có \(C_{98}^3\) cách
d. Chọn anh A và chị B đi chung (nghĩa là chỉ cần chọn 1 người từ 98 người còn lại): \(C_{98}^1\) cách
\(\Rightarrow\) Số cách để anh A và chị B không đi chung là: \(C_{100}^3-C_{98}^1\)
a) Để tính số đoàn đại biểu 3 người có thể thành lập nếu không ai từ chối tham gia, ta sử dụng công thức tổ hợp. Tổng số cách chọn 3 người từ 100 người là:
C3100=100!3!(100−3)!=161700�1003=100!3!(100−3)!=161700b) Để tính số đoàn có thể thành lập nếu có 2 nam và 1 nữ, ta sẽ tính số cách chọn 2 nam từ 60 nam và chọn 1 nữ từ 40 nữ, sau đó nhân kết quả lại với nhau: