Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A = 1 / 50 + 1 / 51 +.....+ 1 / 98 + 1 / 99
Chứng tỏ rằng \(\frac{1}{2}\) < A < 1
mình học vnen nhưng ko có đề toán chỉ có để công dân de day nay về cuộc sống hòa bình và biển hiểu , quyền lợi

1.A. Ta thấy để hàm số xác định thì x-m\(\ne\)0 hay x\(\ne\)m mà vì x\(\in\)(0,1) nên để x\(\ne\)m thì m\(\notin\)(0,1)=>m>=1 hoặc m<=0
2A để A giao B khác 0 thì 2m-1<=m+3 hay m<=4
3C.A giao B =A khi \(\left\{{}\begin{matrix}m< =-1\\m+5>=3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m< =1\\m>=-2\end{matrix}\right.\)


Công thức toán học nằm hết trong phần khoanh đỏ, bạn vào đó tìm hiểu 1 lúc là được:


\(2\frac{4}{5}x-50:\frac{2}{3}=51\)
\(\frac{14}{5}x-50:\frac{2}{3}=51\)
\(\frac{14}{51}x=51+50:\frac{2}{3}\)
\(\frac{14}{51}x=51+75\)
\(\frac{14}{51}x=126\)
\(x=126:\frac{14}{51}\)
\(x=459\)

Từ pt (E) ta xác định được: \(a=5;b=3;c=4\)
\(F_1F_2=2c=8\Rightarrow\) chu vi tam giác \(MF_1F_2=MF_1+MF_2+F_1F_2=2a+2c=18\)
\(\Rightarrow\) nửa chu vi \(p=9\)
Tam giác \(MF_1F_2\) vuông tại M \(\Rightarrow OM=\dfrac{1}{2}F_1F_2=4\)
Gọi \(M\left(x;y\right)\Rightarrow\overrightarrow{OM}=\left(x;y\right)\Rightarrow OM^2=x^2+y^2=16\)
\(\Rightarrow x^2=16-y^2\)
Thay vào pt (E):
\(\dfrac{16-y^2}{25}+\dfrac{y^2}{9}=1\Rightarrow y^2=\dfrac{81}{16}\Rightarrow\left|y\right|=\dfrac{9}{4}\)
\(S_{MF_1F_2}=\dfrac{1}{2}F_1F_2.d\left(M;F_1F_2\right)=\dfrac{1}{2}.2c.\left|y\right|=9\)
\(\Rightarrow r=\dfrac{S_{MF_1F_2}}{p}=1\)
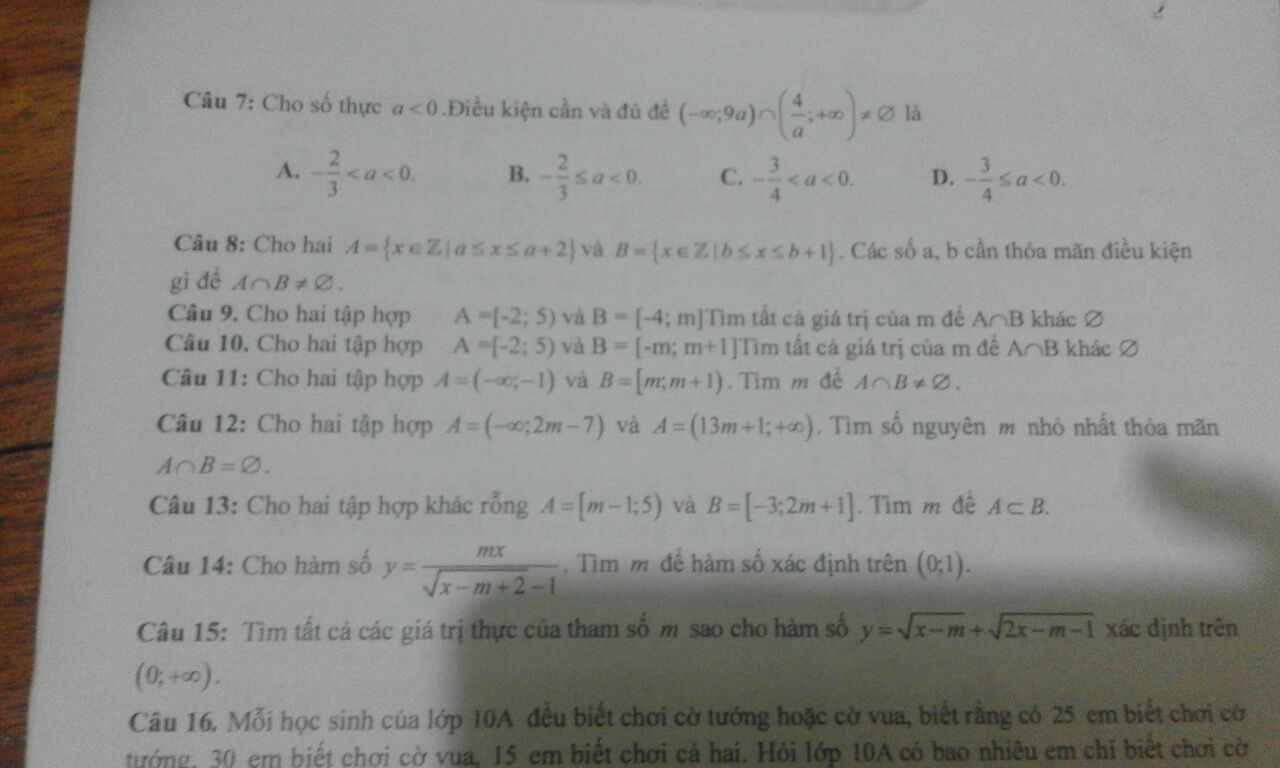 GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!
GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!
Mình chỉ giúp câu 15 thôi :) Bệnh lười ko cho phép mình check mấy câu trên hihi :D
Có \(\pi< \alpha< \frac{3}{2}\pi\Rightarrow\frac{\pi}{2}-\pi>\frac{\pi}{2}-\alpha>\frac{\pi}{2}-\frac{3}{2}\pi\)
\(\Leftrightarrow\frac{-1}{2}\pi>\frac{\pi}{2}-\alpha>-\pi\)
\(\Rightarrow\left(\frac{\pi}{2}-\alpha\right)\in\) góc phần tư thứ 3\(\Rightarrow\sin\left(\frac{\pi}{2}-\alpha\right)< 0\)
\(\pi< \alpha< \frac{3}{2}\pi\Rightarrow2\pi< \pi+\alpha< \frac{5}{2}\pi\)
\(\Rightarrow\left(\pi+\alpha\right)\in\) góc phần tư thứ nhất
\(\Rightarrow\cot\left(\alpha+\pi\right)>0\)
\(\Rightarrow M< 0\)