ND
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DN
4
BT
12 tháng 8 2017
\(\frac{1024}{\left(17x2^5+15x2^5\right)}=\frac{2^{10}}{32x2^5}=\frac{2^{10}}{2^5.2^5}=\frac{2^{10}}{2^{10}}=1\) (1024=210; 32=25)
12 tháng 8 2017
chị giúp nhưng phải k cho c nhé.
\(1024:\left(17x2^5+15x2^5\right)\)
\(=\)\(1024:\left[\left(17+15\right)x2^5\right]\)
\(=1024:\left(32x2^5\right)\)
\(=2^{10}:\left(2^5x2^5\right)\)
\(=2^{10}:2^{10}=1\)
17 tháng 10 2018
a x b = 2/3 = 6/9
a x (b+5) = 28/9
=> 5a = 22/9
=> a = 22/45
b = 15/11
TP
19 tháng 8 2017
Ta có:
\(A=2^1+2^2+2^3+...+2^{100}\)
\(\Rightarrow2A-A=\left(2^2+2^3+2^4+...+2^{101}\right)-\left(2^1+2^2+2^3+...+2^{100}\right)\)
\(\Rightarrow A.\left(2-1\right)=2^2+2^3+2^4+...+2^{101}-2^1-2^2-2^3+...+2^{100}\)
\(\Rightarrow A=\left(2^2-2^2\right)+\left(2^3-2^3\right)+\left(2^4-2^4\right)+...+\left(2^{100}-2^{100}\right)+\left(2^{101}-2^1\right)\)
\(\Rightarrow A=2^{101}-2\Leftrightarrow A=2^x-2\Leftrightarrow x=101\)
DN
19 tháng 8 2017
@Phúc Trần Tấn | Em biết làm ý A rồi nhưng không biết làm ý B.!!
SM
10 tháng 9 2018
- Cạnh huyền góc nhọn: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn tương ứng của tam giác vuông kia thì 2 tam giác đó bằng nhau.
- Cạnh góc vuông-góc nhọn kề: Nếu cạnh huyền và góc nhọn kề của tam giác vuông này bằng cạnh huyền và góc nhọn kề tương ứng của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Thêm một trường hợp khác nhé: cạnh huyền- cạnh góc vuông: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và cạnh góc vuông tương ứng của tam giác vuông kia thì hai tam giác vông đó bằng nhau.
Học tốt
SM
10 tháng 9 2018
Định lí :
Trong tam giác vuông, mỗi cạnh góc vuông bằng :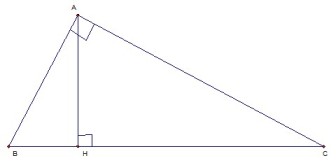
a) Cạnh huyền nhân với sin góc đối hoặc cosin góc kề.
b) Cạnh góc vuông kia nhân với tang góc đối hoặc cotang góc kề.
Công thức :
AC = BC.sin B = BC.cos C = AB.tg B = AB.cotg C.
AB = BC.sin C = BC.cos B = AC. Tam giác C = AC.cotg B
BA
5 tháng 11 2019
\(3+3^2+.....+3^{99}\)
\(=\left(3+3^2+3^3\right)+\left(3^4+3^5+3^6\right)+...+\left(3^{97}+3^{98}+3^{99}\right)\)
\(=39+3^3\left(3+3^2+3^3\right)+........+3^{96}\left(3+3^2+3^3\right)\)
\(=39+3^3\cdot39+...+3^{96}\cdot39\)
\(=39\left(1+3^3+....+3^{96}\right)\)
Vì \(39⋮13\Rightarrow39\in B\left(13\right)\)
16 tháng 8 2018
2 + 4 + 6 + 8 + ... + 90 + 98 + 100
Ta có : 2 + 4 + 6 + 8 + ... + 90 + 98 + 100 (Có 50 số )
= (100 + 2) x 50 : 2
= 2550
16 tháng 8 2018
B1 : Tìm số các số hạng bằng công thức :
( Số cuối - Số đầu ) : khoảng cách + 1
=> ( 100 - 2 ) : 2 + 1 = 50 ( số )
B2 : Tính tổng bằng công thức :
( Số đầu + Số cuối ) x Số các số hạng : 2
=> ( 100 + 2 ) x 50 : 2 = 2550
Hok tốt ^^
28 tháng 11 2015
n2 + n + 1 = n(n+1) + 1
Ta có n(n+1) là tích của 2 số tự nhiên liên tiếp
Nên n(n+1) không có tận cùng là 4 hoặc 9
=> n(N+1) + 1 không có ận cùng là 5 hoặc 0
Vậy n2 + n + 1 không chia hết cho 15 (dpcm)
D
1
10 tháng 10 2023
Bài 1.
a,Vì \(\dfrac{a}{b}>1\)=>a<b
Với m∈N* Ta có
\(am> bm\)=>\(am+ab> bm+ab\)=>\(a\left(b+m\right)> b\left(a+m\right)\)=>\(\dfrac{a}{b}>\dfrac{a+m}{b+m} \)
b, Vì \(\dfrac{a}{b}< 1\)=>a<b
Với m∈N* =>
\(am< bm\)=>\(am+ab< bm+ab\)=>\(a\left(b+m\right)< b\left(a+m\right)\)=>\(\dfrac{a}{b}<\dfrac{a+m}{b+m} \)
Tự áp dụng cho bài 2 nhé bạn :)