
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)

`a)m=0=>x^2-x+3=0<=>(x-1/2)^2+11/4=0` (Vô lí)
`=>m=0` ptr vô nghiệm
`b)` Ptr có nghiệm kép `<=>\Delta=0`
`<=>[-(2m+1)]^2-4(m^2+3)=0`
`<=>4m^2+4m+1-4m^2-12=0`
`<=>4m-11=0`
`<=>m=11/4`
`c)` Ptr có `2` nghiệm pb`<=>\Delta > 0`
`<=>4m-11 > 0<=>m > 11/4`
`d)` Ptr vô nghiệm `<=>\Delta < 0<=>4m-11 < 0<=>m < 11/4`
Bài 2:
a: Khi m=0 thì pt sẽ là:
\(x^2-x+3=0\)
=>\(x\in\varnothing\)
b: \(\Delta=\left(2m+1\right)^2-4\left(m^2+3\right)\)
=4m^2+4m+1-4m^2-12
=4m-11
Để pt có nghiệm kép thì 4m-11=0
=>m=11/4
c: Để phương trình có hai nghiệm pb thì 4m-11>0
=>m>11/4
d: Để pt vô nghiệm thì 4m-11<0
=>m<11/4

Phần trắc nghiệm:
Hàm số bậc nhất biến $x$ có dạng $y=ax+b$ với $a, b\in\mathbb{R}, a\neq 0$.
1. A
2. C
3. A
4. B
5. B
6. A
7. B
8. C

a: \(4-\sqrt{3-2x}=0\)
\(\Leftrightarrow3-2x=16\)
hay \(x=-\dfrac{13}{2}\)

a: góc BEC=góc BFC=90 độ
=>BFEC nội tiếp
góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b: góc ABT=1/2*180=90 độ
=>BT vuông góc AB
=>BT//CH
góc ACT=1/2*180=90 độ
=>AC vuông góc CT
=>CT//BH
mà BT//CH
nên BHCT là hình bình hành

\(2\sqrt{9\left(x-3\right)}-\sqrt{4\left(x-3\right)}=10+\frac{1}{2}\)
\(6\sqrt{\left(x-3\right)}-2\sqrt{\left(x-3\right)}=\frac{21}{2}\)
\(4\sqrt{\left(x-3\right)}=\frac{21}{2}\)
\(\sqrt{\left(x-3\right)}=\frac{21}{8}\)
\(x-3=\frac{441}{64}\)
\(x=\frac{633}{64}\)
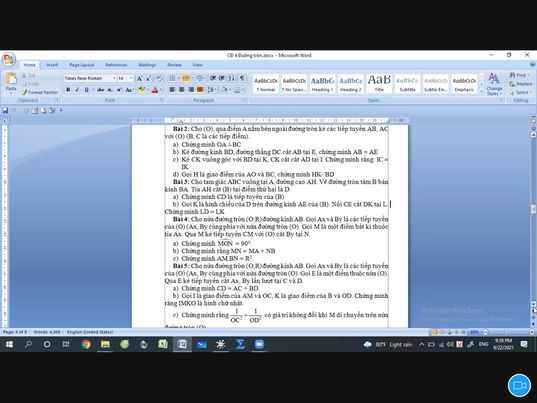
 Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
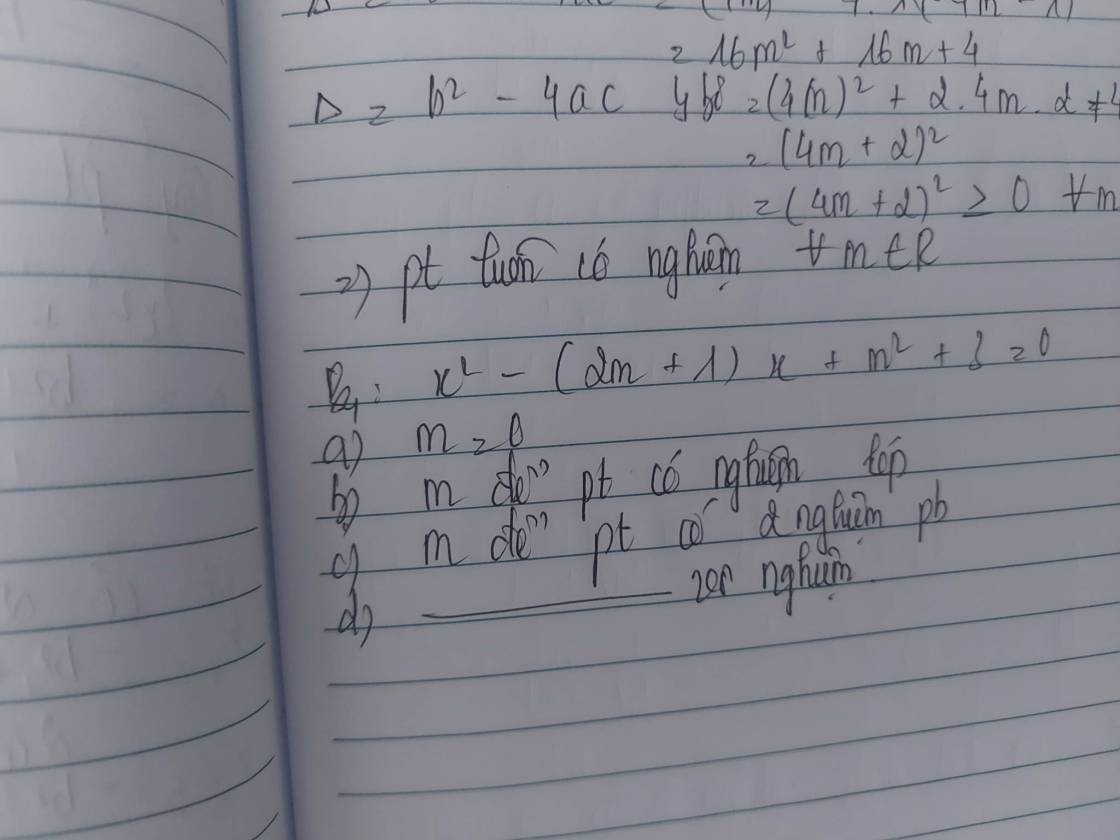


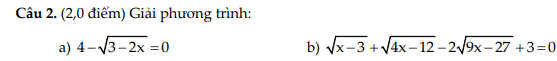

\(\Delta'=\left(m+1\right)^2-\left(-2m-3\right)=m^2+2m+1+2m+3\)
\(=m^2+4m+4=\left(m+2\right)^2\ge0\)
Vậy pt luôn có 2 nghiệm x1;x2