K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 12 2022
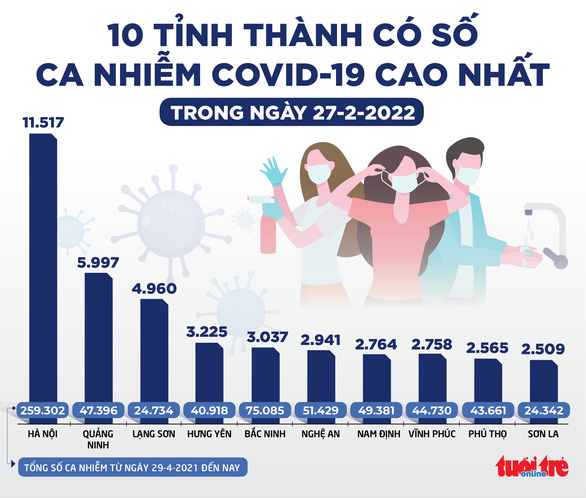
a. Những tỉnh thành phố có ca nhiễm hơn 2800 ca: Nghệ An, Bắc Ninh, Hưng Yên, Lạng Sơn, Quảng Ninh, Hà Nội.
b. Tỉnh có số ca nhiễm Covid 19 cao nhất là: Hà Nội
KV
25 tháng 1 2024
\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)
Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:
\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)
\(\dfrac{9y^2}{25}-y^2=-4\)
\(-\dfrac{16}{25}y^2=-4\)
\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)
\(y^2=\dfrac{25}{4}\)
\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)
*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)
*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)
Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)
AH
Akai Haruma
Giáo viên
31 tháng 1 2024
Lời giải:
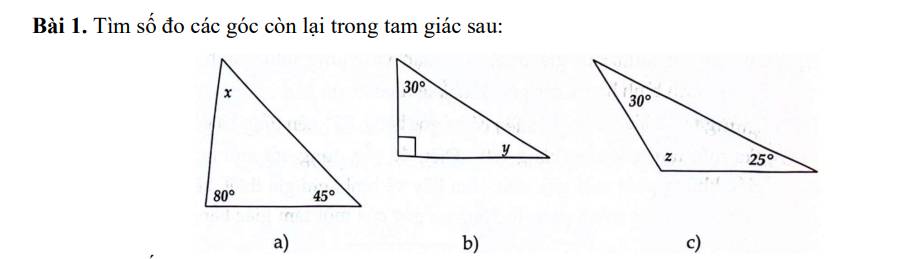
Áp dụng tính chất tổng 3 góc trong một tam giác bằng $180^0$
a.
$x=180^0-80^0-45^0=55^0$
b.
$y=180^0-30^0-90^0=60^0$
c.
$z=180^0-30^0-25^0=125^0$
TC
4
22 tháng 12 2022
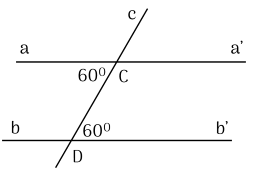
Ta có: góc aCd = góc CDb' (=60°)
Mà 2 góc này ở vị trí so le trong
=> aa' // bb'
TC
6
22 tháng 12 2022
Xét ∆ABC và ∆DBC có:
AB = BD
Góc ABC = góc CBD
Góc BAC = góc BDC
=> ∆ABC = ∆DBC
18 tháng 9 2023
Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:
\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh
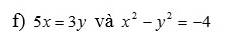
a.
\(A\in Z\Rightarrow2A\in Z\Rightarrow\dfrac{2\left(3x-2\right)}{2x-3}\in Z\)
\(\Rightarrow\dfrac{6x-4}{2x-3}\in Z\Rightarrow\dfrac{3\left(2x-3\right)+5}{2x-3}\in Z\)
\(\Rightarrow3+\dfrac{5}{2x-3}\in Z\Rightarrow\dfrac{5}{2x-3}\in Z\)
\(\Rightarrow2x-3=Ư\left(5\right)=\left\{-5;-1;1;5\right\}\)
\(\Rightarrow x=\left\{-1;1;2;4\right\}\)
Thử lại thấy đều thỏa mãn
b.
\(\dfrac{2x+4}{y}-\dfrac{2}{x}-\dfrac{5}{xy}=1\)
\(\Rightarrow x\left(2x+4\right)-2y-5=xy\)
\(\Leftrightarrow2x^2+4x-y-5=xy\)
\(\Leftrightarrow2x^2+4x-5=y\left(x+1\right)\)
Với \(x=-1\) không thỏa mãn
Với \(x\ne-1\Rightarrow y=\dfrac{2x^2+4x-5}{x+1}\) (1)
Do \(y\in Z\Rightarrow\dfrac{2x^2+4x-5}{x+1}\in Z\Rightarrow\dfrac{2x^2+4x+2-7}{x+1}\in Z\)
\(\Rightarrow\dfrac{2\left(x+1\right)^2-7}{x+1}\in Z\Rightarrow2\left(x+1\right)-\dfrac{7}{x+1}\in Z\)
\(\Rightarrow\dfrac{7}{x+1}\in Z\) do \(2\left(x+1\right)\in Z\) với \(x\in Z\)
\(\Rightarrow x+1=Ư\left(7\right)=\left\{-7;-1;1;7\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x=-8\left(loại\right)\\x=-2\left(loại\right)\\x=0\\x=6\end{matrix}\right.\)
Thế vào (1): \(\left[{}\begin{matrix}x=0\Rightarrow y=-5< 0\left(loại\right)\\x=6\Rightarrow y=13\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(6;13\right)\)