

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Diện tích xung quanh của cái lọ là:
S
x
q
= 2
π
r.h= 2.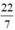 .14.10 = 880 (
c
m
2
)
.14.10 = 880 (
c
m
2
)
Diện tích đáy lọ là :
S
đ
á
y
=
π
.
R
2
= 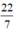 .142 = 616 (
c
m
2
)
.142 = 616 (
c
m
2
)
Diện tích xung quanh cộng với diện tích một đáy là:
S = S x q + S đ á y = 880 + 616 = 1496 ( c m 2 )
Vậy chọn đáp án E

a) Với giả thiết ở đề bài, ta có thể tính được r từ đó tính được diện tích mặt cầu gần bằng \(26cm^2\)
b) Tương tự câu a, ta tính được thể tích hình nón là \(7,9cm^3\)

Gọi R là bán kính đáy hộp sữa
\(\Rightarrow\)chiều cao hộp sữa là : \(3R\)
Thể tích hộp sữa là : \(\pi R^2\times3R=192\pi\Leftrightarrow R^3=64\Leftrightarrow R=4cm\)
Ơ mà sao lại hỏi thể tích nhỉ, đề cho luôn là \(192\pi cm^3\) mà nhỉ

Áp dụng BĐT sau:\(2\left(a^2+b^2\right)\ge\left(a+b\right)^2\) ( dùng BĐT Bunhiacopski mà chứng minh :D )
Ta có:\(\frac{a+b}{a^2+b^2}=\frac{41}{9}\Rightarrow\frac{a^2+b^2}{a+b}=\frac{41}{9}\)
\(\Rightarrow\frac{82}{9}=\frac{2\left(a^2+b^2\right)}{a+b}\ge\frac{\left(a+b\right)^2}{a+b}=a+b\)
\(\Rightarrow a+b\le9\)
Mặt khác:\(41\left(a+b\right)=9\left(a^2+b^2\right);\left(41;9\right)=1\Rightarrow a+b⋮9\Rightarrow a+b=9\)
\(\Rightarrow a^2+b^2=41\)
Ta có hệ:\(\hept{\begin{cases}a+b=9\\a^2+b^2=41\end{cases}}\) giải cái hệ này là ra a,b nha < 3