
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\Rightarrow\left|\dfrac{3}{4}+x\right|=0\Rightarrow\dfrac{3}{4}+x=0\Rightarrow x=-\dfrac{3}{4}\)
b) \(\Rightarrow x+0,4=\dfrac{4}{9}:\dfrac{2}{3}=\dfrac{2}{3}\Rightarrow x=\dfrac{2}{3}-0,4=\dfrac{4}{15}\)

\(=\dfrac{101}{2}\left(4+\dfrac{5}{3}-2-\dfrac{5}{3}\right)=\dfrac{101}{2}\cdot2=101\)

a: Ta có: \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
\(\widehat{ACB}=\widehat{ECN}\)(hai góc đối đỉnh)
Do đó: \(\widehat{ABC}=\widehat{ECN}\)
Xét ΔMBD vuông tại D và ΔNCE vuông tại E có
BD=CE
\(\widehat{MBD}=\widehat{NCE}\)
Do đó: ΔMBD=ΔNCE
=>DM=EN
b: Ta có: DM\(\perp\)BC
EN\(\perp\)BC
Do đó: DM//EN
Xét ΔIDM vuông tại D và ΔIEN vuông tại E có
MD=EN
\(\widehat{MDI}=\widehat{ENC}\)(hai góc so le trong, DM//EN)
Do đó: ΔIDM=ΔIEN
=>IM=IN
=>I là trung điểm của MN

Câu 5:
Xét ΔABC có AB=AC<BC
mà \(\widehat{ACB};\widehat{ABC};\widehat{BAC}\) lần lượt là góc đối diện của các cạnh AB,AC,BC
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)

Bài 5:
d: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y-z}{2+3-4}=\dfrac{-20}{1}=-20\)
Do đó: x=-40; y=-60; z=-80

a: góc BAH=90-50=40 độ
Xét ΔABM và ΔDCM có
AB=DC
góc ABM=góc DCM
MB=MC
Do đó: ΔABM=ΔDCM
b: ΔABM=ΔDCM
=>góc AMB=góc DMC
=>góc DMC+góc CMA=180 độ
=>A,M,D thẳng hàng
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hbh
=>BD//AC

2:
a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
ΔBAD cân tại B có BE là phân giác
nên BE vuông góc AD
b: Xét ΔBAE và ΔBDE có
BA=BD
góc ABE=góc DBE
BE chung
=>ΔBAE=ΔBDE
=>EA=ED
=>ΔEAD cân tại E
c: Xét ΔEAF vuông tại A và ΔEDC vuông tại D có
EA=ED
AF=DC
=>ΔEAF=ΔEDC
=>EF=EC
=>ΔECF cân tại E
d: ΔEAF=ΔEDC
=>góc AEF=góc DEC
=>góc AEF+góc AED=180 độ
=>D,E,F thẳng hàng




 mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33
mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33 
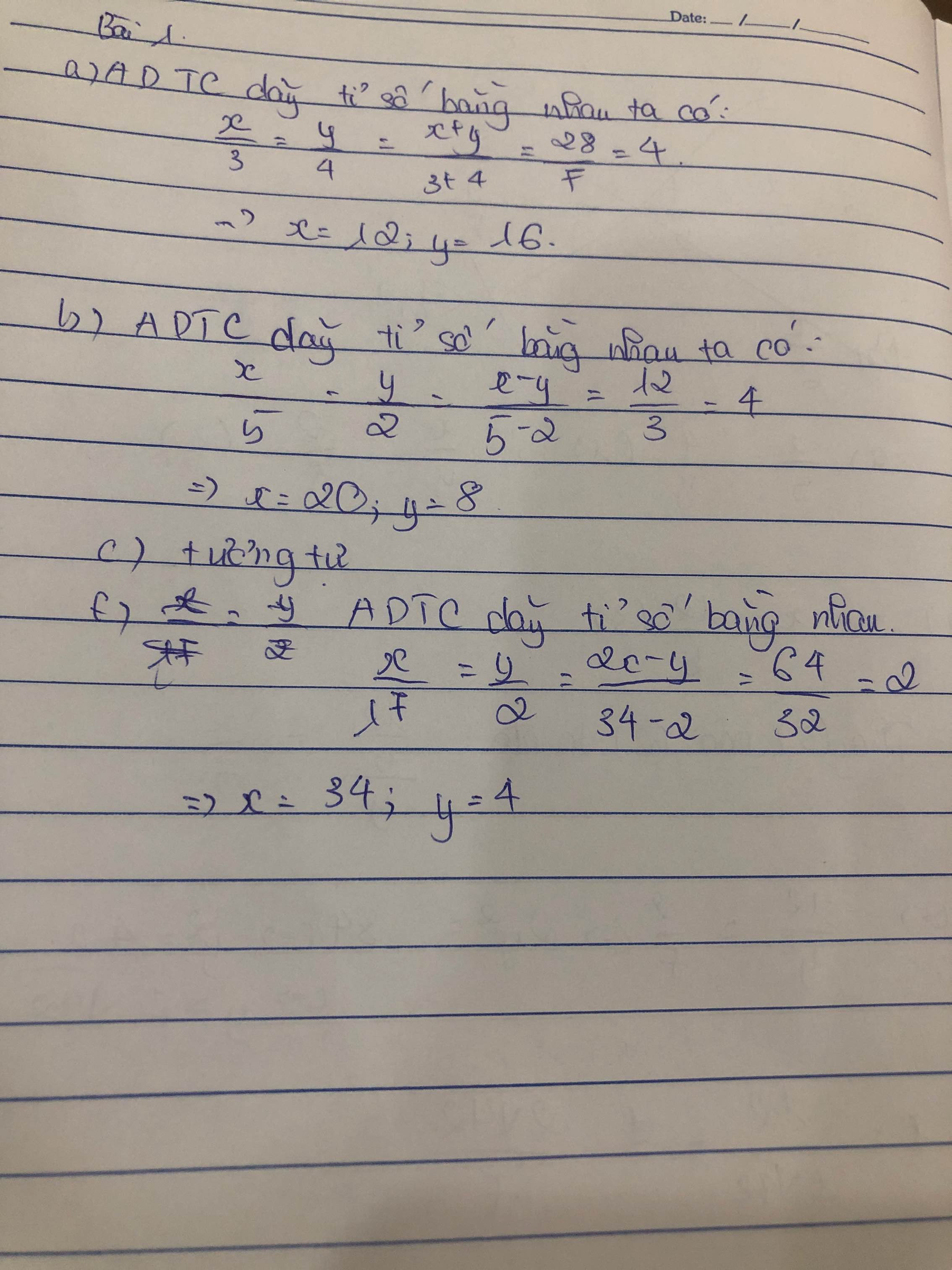
 Mng giúp mik vs ạ
Mng giúp mik vs ạ
Giúp j