
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(S_{ABCD}=\dfrac{AD\cdot DC}{2}=\dfrac{12\cdot16}{2}=12\cdot8=96\left(cm^2\right)\)
b: MD=6cm
DO=5cm


Bài 1:
Vận tốc cano khi dòng nước lặng là: $25-2=23$ (km/h)
Bài 2:
Đổi 1 giờ 48 phút = 1,8 giờ
Độ dài quãng đường AB: $1,8\times 25=45$ (km)
Vận tốc ngược dòng là: $25-2,5-2,5=20$ (km/h)
Cano ngược dòng từ B về A hết:
$45:20=2,25$ giờ = 2 giờ 15 phút.

Bài 1:
a.
$a^3-a^2c+a^2b-abc=a^2(a-c)+ab(a-c)$
$=(a-c)(a^2+ab)=(a-c)a(a+b)=a(a-c)(a+b)$
b.
$(x^2+1)^2-4x^2=(x^2+1)^2-(2x)^2=(x^2+1-2x)(x^2+1+2x)$
$=(x-1)^2(x+1)^2$
c.
$x^2-10x-9y^2+25=(x^2-10x+25)-9y^2$
$=(x-5)^2-(3y)^2=(x-5-3y)(x-5+3y)$
d.
$4x^2-36x+56=4(x^2-9x+14)=4(x^2-2x-7x+14)$
$=4[x(x-2)-7(x-2)]=4(x-2)(x-7)$
Bài 2:
a. $(3x+4)^2-(3x-1)(3x+1)=49$
$\Leftrightarrow (3x+4)^2-[(3x)^2-1]=49$
$\Leftrightarrow (3x+4)^2-(3x)^2=48$
$\Leftrightarrow (3x+4-3x)(3x+4+3x)=48$
$\Leftrightarrow 4(6x+4)=48$
$\Leftrightarrow 6x+4=12$
$\Leftrightarrow 6x=8$
$\Leftrightarrow x=\frac{4}{3}$
b. $x^2-4x+4=9(x-2)$
$\Leftrightarrow (x-2)^2=9(x-2)$
$\Leftrightarrow (x-2)(x-2-9)=0$
$\Leftrightarrow (x-2)(x-11)=0$
$\Leftrightarrow x-2=0$ hoặc $x-11=0$
$\Leftrightarrow x=2$ hoặc $x=11$
c.
$x^2-25=3x-15$
$\Leftrightarrow (x-5)(x+5)=3(x-5)$
$\Leftrightarrow (x-5)(x+5-3)=0$
$\Leftrightarrow (x-5)(x+2)=0$
$\Leftrightarrow x-5=0$ hoặc $x+2=0$
$\Leftrightarrow x=5$ hoặc $x=-2$

\(a,\) Vì ABCD là hbh nên \(AD=BC;AB//CD\Rightarrow\widehat{ADB}=\widehat{CBD}\left(so.le.trong\right)\)
Ta có \(\left\{{}\begin{matrix}\widehat{AED}=\widehat{CFB}\left(=90^0\right)\\\widehat{ADB}=\widehat{CBD}\left(cm.trên\right)\\AD=BC\left(cm.trên\right)\end{matrix}\right.\) nên \(\Delta AED=\Delta CFB\left(ch-gn\right)\)
\(\Rightarrow DE=BF\left(1\right)\)
Mà O là giao 2 đường chéo hbh ABCD nên O là trung điểm AC,BD
\(\Rightarrow OB=OD\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\Rightarrow OB-BF=OD-DE\Rightarrow OE=OF\)
\(b,\) Xét tg AECF có O là trung điểm AC,EF nên là hbh

-Hình vẽ:
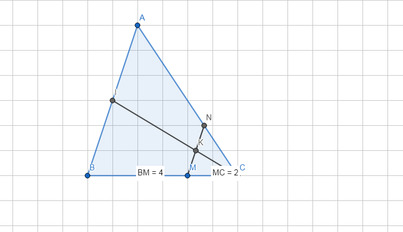
a) Ta có: \(\dfrac{CM}{BM}=\dfrac{1}{2}\Rightarrow\dfrac{BM}{CM}=2\).
-Xét △ABC có: \(\dfrac{BM}{CM}=\dfrac{AN}{NC}=2\) .
\(\Rightarrow MN\)//\(AB\) (định lí Ta-let đảo).
b) -Xét △BCI có: MK//BI (cmt).
\(\Rightarrow\dfrac{MK}{BI}=\dfrac{CK}{CI}\) (định lí Ta-let) (1).
-Xét △ACI có: NK//AI (cmt).
\(\Rightarrow\dfrac{NK}{AI}=\dfrac{CK}{CI}\) (định lí Ta-let) (2).
-Từ (1) và (2) suy ra: \(\dfrac{MK}{BI}=\dfrac{NK}{AI}\)
Mà \(BI=AI\) (I là trung điểm AB).
\(\Rightarrow MK=NK\) hay K là trung điểm MN.

Gọi chiều rộng ban đầu là x
Chiều dài ban đầu là x+5
Theo đề, ta có:
(x+3)(x+2)=x(x+5)-16
\(\Leftrightarrow x^2+5x+6-x^2-5x+16=0\)
=>22=0(vô lý)
=>Đề sai rồi bạn

a: Xét tứ giác AIHK có
\(\widehat{AIH}=\widehat{AKH}=\widehat{KAI}=90^0\)
Do đó: AIHK là hình chữ nhật







a: AE=1/3x6=2(cm)
b: AE/AB=AF/AC
c: Xét ΔABC có EF//BC
nên AE/AB=AF/AC
=>AF/7=1/3
hay AF=7/3(cm)