Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta co: 6x-2y=x+y(nhan cheo)
\(\Rightarrow\)5x=3y
\(\Rightarrow\)x/y=3/5

câu 3 : kq 2 phần 3
câu 4 : kq -1
câu 5 : kq -8 phần 3
câu 6 : kq 4 phần 3
câu 7 : kq -3
câu 9 : x = 1 phần 2
câu 10 : kq x =13 phần 12
câu 12 : 2 mũ 3 phần 3 mũ 3 = 8 phần 27
câu 13 : câu D nha
câu 10 ; 12 mình ko trắc lắm đâu nha
còn câu 8 mình ko rỏ mình sẻ tính lại sau

1: Xét ΔAOC và ΔBOD có
OA=OB
\(\widehat{AOC}=\widehat{BOD}\)
OC=OD
Do đó: ΔAOC=ΔBOD
Suy ra: \(\widehat{ACO}=\widehat{BDO}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD

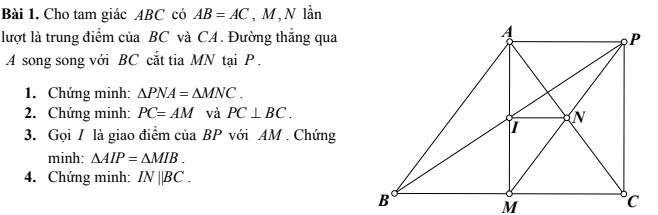
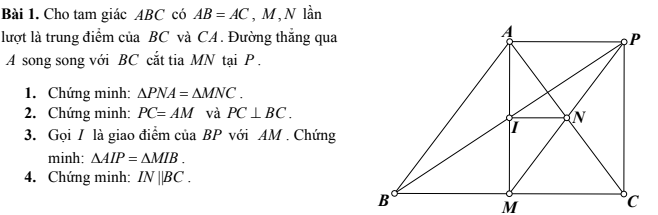
1. Vì N là trung điểm của AC do đó AN = CN
Ta có P là điểm kéo dài từ A cắt tia MN nên M, N, P là 3 điểm thẳng hàng
\(\Rightarrow\)N là trung điểm của MP và MN = NP
Xét \(\Delta PNA\) và \(\Delta MNC\) ta có :
AN = NC (cmt)
\(\widehat{PNA}\) = \(\widehat{MNC}\) ( hai góc đối đỉnh )
MN = NP (cmt)
\(\Rightarrow\Delta PNA=\Delta MNC\) ( c.g.c )
\(\Rightarrow AP=MC\) ( hai cạnh tương ứng )
2. Xét \(\Delta ANM\) và \(\Delta PNC\) ta có :
AN = NC (cmt)
\(\widehat{ANM}\) = \(\widehat{PNC}\) ( hai góc đối đỉnh )
MN = NP (cmt)
\(\Rightarrow\Delta ANM=\Delta PNC\) ( c.g.c )
\(\Rightarrow AM=PC\) ( hai cạnh tương ứng )
\(\Rightarrow AM\)//\(PC\)
Vì \(\Delta ABC\) có AB = AC nên \(\Delta ABC\) là tam giác cân tại A
Mà M là trung điểm của BC \(\Rightarrow BM=MC\) nên AM là đường trung trực của đoạn thẳng BC hay AM ⊥ BC
Áp dụng theo quan hệ giữa tính vuông góc và tính song song "nếu a//b và c⊥a thì b⊥c"
Từ đó ta suy ra PC ⊥ BC
2. Vì AP = MC nên AP = BM ( cùng MC )
Điểm I được nối qua N và nằm trên đoạn thẳng AM nên ba điểm A, I, M thẳng hàng ⇒ I là trung điểm của AM và AI = IM
Xét \(\Delta AIP\) và \(\Delta MIB\) ta có :
AP = PM (cmt)
AI = IM (cmt)
\(\Rightarrow\Delta AIP=\Delta MIB\) ( trường hợp bằng nhau hai cạnh góc vuông của tam giác vuông )
*Thưa bạn, câu 4 mình không biết giải nên mong bạn thông cảm. Nếu bài mình có chỗ nào không đúng thì bạn sửa lại giúp mình nhé!

1: Xét ΔABC có AB=AC
nên ΔBAC cân tại A
Suy ra: \(\widehat{B}=\widehat{C}\)
Ta có: ΔABC cân tại A
mà AH là đường trung tuyến ứng với cạnh đáy BC
nên AH là đường cao ứng với cạnh BC

4: Xét ΔAMC có
I là trung điểm của AM
N là trung điểm của AC
Do đó: IN là đường trung bình của ΔAMC
Suy ra: IN//MC
hay IN//BC