Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 8:
Giải:
Ta có: \(a:b=3:4\Rightarrow\frac{a}{3}=\frac{b}{4}\Rightarrow\frac{a^2}{9}=\frac{b^2}{16}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a^2}{9}=\frac{b^2}{16}=\frac{a^2+b^2}{9+16}=\frac{36}{25}\)
+) \(\frac{a^2}{9}=\frac{36}{25}\Rightarrow a^2=\frac{324}{25}\Rightarrow a=\pm\frac{18}{5}\)
+) \(\frac{b^2}{16}=\frac{36}{25}\Rightarrow b^2=\frac{576}{25}\Rightarrow b=\pm\frac{24}{5}\)
Vậy bộ số \(\left(x;y\right)\) là \(\left(\frac{18}{5};\frac{24}{5}\right);\left(\frac{-18}{5};\frac{-24}{5}\right)\)

a: =>5x=3x-6
=>2x=-6
hay x=-3
b: \(\Leftrightarrow\left(x-3\right)^2=4\cdot5^2=100\)
=>x-3=10 hoặc x-3=-10
=>x=13 hoặc x=-7
c: \(\left|x^3+1\right|+2\ge2\forall x\)
Dấu '=' xảy ra khi x=-1

Bài 3:
a: Ta có: \(A=5+5^2+5^3+...+5^8\)
\(=\left(5+5^2\right)+5^2\left(5+5^2\right)+5^4\left(5+5^2\right)+5^6\left(5+5^2\right)\)
\(=30\left(1+5^2+5^4+5^6\right)⋮30\)
b: \(B=3+3^3+3^5+...+3^{29}\)
\(=\left(3+3^3+3^5\right)+3^6\left(3+3^3+3^5\right)+...+3^{24}\left(3+3^3+3^5\right)\)
\(=273\left(1+3^6+...+3^{24}\right)⋮273\)

a) Số cần tìm là:
\(7,2:\dfrac{2}{3}=\dfrac{54}{5}\)
b) Số cần tìm là:
\(\left(-5\right):1\dfrac{3}{7}=\left(-5\right):\dfrac{10}{7}=-\dfrac{7}{2}\)
a/ Gọi số cần tìm là x.
Theo đề bài ta có:
x . \(\dfrac{2}{3}=7,2\)
x = 7,2 : \(\dfrac{2}{3}\)
x = \(\dfrac{36}{5}.\dfrac{3}{2}\)
x = \(\dfrac{54}{5}=10,8.\)
Vậy \(\dfrac{2}{3}\) của nó là \(\dfrac{2}{3}\) của 10,8 bằng 7,2.
b/ Gọi số cần tìm là x.
Theo đề bài ta có:
x . \(1^3_7=-5\)
x . \(\dfrac{10}{7}\) = -5
x = -5 : \(\dfrac{10}{7}\)
x = -5 . \(\dfrac{7}{10}\)
x = \(\dfrac{-7}{2}\)= -3,5.
Vậy \(1\dfrac{3}{7}\) của nó là của -3,5 bằng -5.


1/
a/ A = 1 + 3 + 3^2 + 3^3 + ... + 3^119
=> 3A = 3 + 3^2 + 3^3 + 3^4 + ... + 3^120
=> 3A - A = 3 + 3^2 + 3^3 + 3^4 + ... + 3^120 - (1 + 3 + 3^2 + 3^3 + ... + 3^119)
=> 2A = 3^120 - 1
=> A = (3 ^120 - 1)/2
b/ 2A + 1 = 27x
<=> 3^120 = 27x
<=> 27^40 = 27x
<=> x = 40
c/ +) A = 1 + 3 + 3^2 + 3^3 + ... + 3^119
= (1 + 3^2) + (3 + 3^3) + (3^4 + 3^6) + ...+ (3^117 + 3^119)
= 1+ 3^2 + 3(1+ 3^2) + 3^4(1 + 3^2) ...+ 3^117( 1+ 3^2)
= (1 + 3^2) (1 + 3 + 3^4+ ...+ 3^117)
= 10 * (1 + 3 + 3^4+ ...+ 3^117) \(⋮\) 5
+) A = 1 + 3 + 3^2 + 3^3 + ... + 3^119
= (1 + 3 + 3^2) + (3^3 + 3^4 + 3^5) + ...+ (3^117 + 3^118 + 3^119)
= (1 + 3 + 3^2) + 3^3 (1+ 3 + 3^2) + ...+ 3^117 (1+ 3 + 3^2)
= (1 + 3 + 3^2) (1+ 3^3 +... + 3^117)
= 13 * (1+ 3^3 +... + 3^117) \(⋮\)13

Câu 2:
a: \(\Leftrightarrow12x-60=7x-5\)
=>5x=55
=>x=11
b: \(\Leftrightarrow\left(2x-3\right)^{2010}\left[\left(2x-3\right)^2-1\right]=0\)
=>(2x-3)(2x-2)(2x-4)=0
hay \(x\in\left\{\dfrac{3}{2};1;2\right\}\)

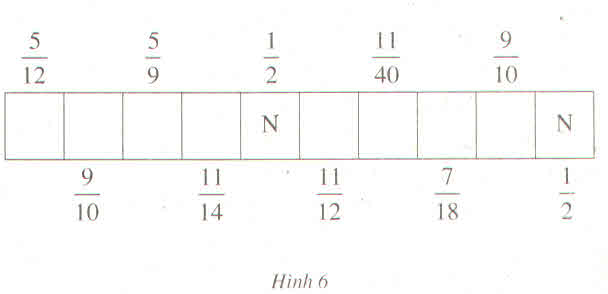
 Đó là hai địa danh HỘI AN và MỸ SƠN của Viêt Nam được UNESCO công nhân là di sản văn hóa thế giới vào năm 1999.
Đó là hai địa danh HỘI AN và MỸ SƠN của Viêt Nam được UNESCO công nhân là di sản văn hóa thế giới vào năm 1999.