K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DV
2 tháng 11 2017
\(P=\sqrt{\left(x-\dfrac{3}{4}\right)^2}+\dfrac{1}{4}\)
\(=\left|x-\dfrac{3}{4}\right|+\dfrac{1}{4}\)
Ta có : \(\left|x-\dfrac{3}{4}\right|\ge0\forall x\Rightarrow\left|x-\dfrac{3}{4}\right|+\dfrac{1}{4}\ge\dfrac{1}{4}\forall x\)
\(\Rightarrow P\ge\dfrac{1}{4}\)
Dấu "=" xảy ra
\(\Leftrightarrow x-\dfrac{3}{4}=0\Leftrightarrow x=\dfrac{3}{4}\)
Vậy GTNN của P là \(\dfrac{1}{4}\) khi x = \(\dfrac{3}{4}\)
2 tháng 3 2017
Ta có: \(\left|x-1\right|+\left|x-5\right|=\left|x-1\right|+\left|5-x\right|\)
Nhận thấy: \(\left[{}\begin{matrix}\left|x-1\right|\ge x-1\\\left|5-x\right|\ge5-x\end{matrix}\right.\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge x-1+5-x\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge4\)
Dấu \("="\) xảy ra khi:
\(\left[{}\begin{matrix}x-1\ge0\\5-x\ge0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le5\end{matrix}\right.\) \(\Rightarrow1\le x\le5\)
Vậy \(1\le x\le5.\)
2 tháng 3 2017
Cho mk thêm cái ạ:
\(x\in\left\{1;2;3;4;5\right\}\)
Vậy \(x\in\left\{1;2;3;4;5\right\}\)
17 tháng 5 2022
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
BD=CE
\(\widehat{ABD}=\widehat{ACE}\)
Do đó: ΔABD=ΔACE
Suy ra: AB=AC
hay ΔABC cân tại A
b: XétΔABC có
AD là đường cao
CH là đường cao
AD cắt CH tại D
Do đó: D là trực tâm của ΔABC
=>BD vuông góc với AC
5 tháng 4 2017
a) \(\left(x-3\right)\left(x-2\right)< 0\)
Ta có : \(x-2>x-3\)
\(\Rightarrow\left\{{}\begin{matrix}x-3< 0\\x-2>0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x< 3\\x>2\end{matrix}\right.\Rightarrow2< x< 3\)
Vậy \(2< x< 3\)
b) \(3x+x^2=0\)
\(x\left(3+x\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\3+x=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\)
Vậy \(x\in\left\{-3;0\right\}\)
DT
1
MV
6 tháng 8 2017
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\dfrac{x+y}{5}=\dfrac{x-y}{8}=\dfrac{x+y+x-y}{5+8}=\dfrac{2x}{13}=\dfrac{4x}{26}\)
Ta có:
\(\dfrac{x+y}{5}=\dfrac{xy}{26};\dfrac{x+y}{5}=\dfrac{4x}{26}\\ \Rightarrow\dfrac{xy}{26}=\dfrac{4x}{26}\Rightarrow y=4\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\dfrac{x+y}{5}=\dfrac{x-y}{8}=\dfrac{x+y-x+y}{5-8}=\dfrac{2y}{-3}\)
Ta có:
\(\dfrac{x-y}{8}=\dfrac{xy}{26};\dfrac{x-y}{8}=\dfrac{2y}{-3}\\ \Rightarrow\dfrac{xy}{26}=\dfrac{2y}{-3}\Rightarrow-3xy=52y\Leftrightarrow-3x=52\Rightarrow x=\dfrac{-52}{3}\)
Vậy \(x=-\dfrac{52}{3};y=4\)
19 tháng 3 2017
Ta có:\(2009^{20}=\left(2009^2\right)^{10}=4036081^{10}< 20092009^{10}\)
Vậy \(2009^{20}< 20092009^{10}\)
help me
H
25 tháng 7 2017
Theo mình nghĩ thì đề thiếu là tam giác ABC vuông tại A nhé!
Bạn xem lại đề!:)
1 tháng 2 2017
hé hé bạn mik ớ ngân giới tính rất linh hoạt
P/s : đầu óc bạn thì ko đc linh hoạt bởi tên ngân còn hỏi là trai hay gái
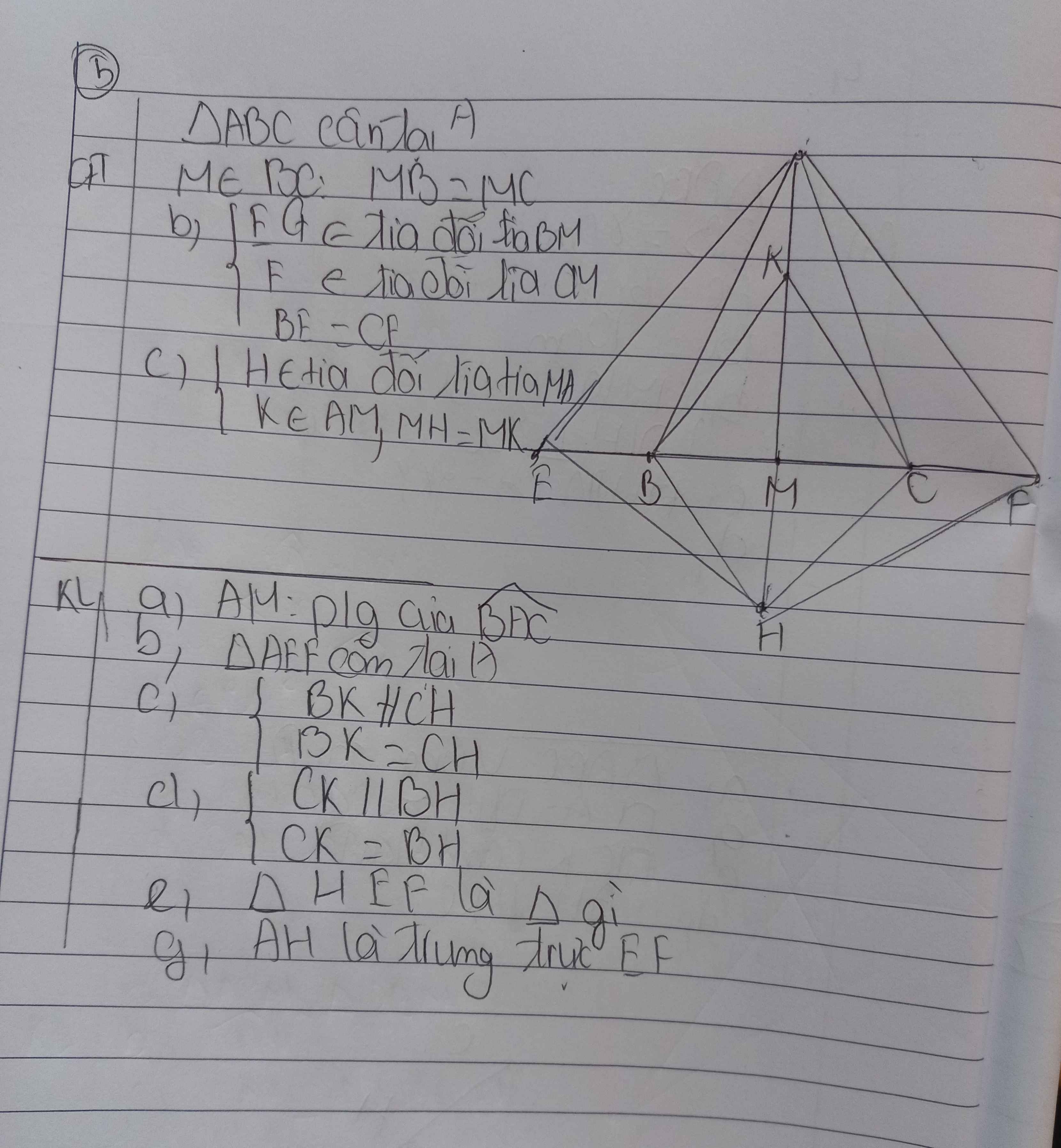
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
b: Xét ΔABE và ΔACF có
AB=AC
\(\widehat{ABE}=\widehat{ACF}\)
BE=CF
Do đó: ΔABE=ΔACF
c: Xét tứ giác BKCH có
M là trung điểm của BC
M là trung điểm của HK
Do đó: BKCH là hình bình hành
Suy ra: BK//CH; BK=CH
d: Ta có: BKCH là hình bình hành
nên CK//BH; CK=BH