Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Vì M và N là hai điểm gần nhau nhất trên phương truyền sóng và dao động ngược pha với nhau nên khoảng cách giữa hai vị trí cân bằng của M và N là λ 2
Vì M và N ngược pha nên khoảng cách xa nhất và gần nhất giữa hai điểm M và N là:
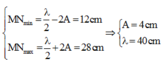
Tần số: 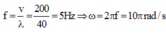
Tốc độ dao động cực đại của một điểm trên phương truyền sóng:
![]()

Chu kì \(T=2\pi/\omega=2s\)
Bước sóng: \(\lambda=v.T=20.2=40cm\)
M cùng pha với O suy ra \(OM=k\lambda=40k(cm)\)
NM gần nhau nhất dao động vuông pha suy ra \(MN=\dfrac{\lambda}{4}=10cm\)
Căn cứ theo các đáp án ta có thể chọn C là đáp án đúng.

Đề nghị bạn gửi mỗi bài một câu thôi, nhìn thế này hoa mắt quá :)
1. Chu kì sóng: \(T=\frac{2\pi}{\omega}=\frac{2\pi}{4\pi}=0,5s\)
Bước sóng: \(\lambda=v.T=12.0,5=6m\)
Độ lệch pha giữa 2 điểm: \(\Delta\varphi=\frac{2\pi d}{\lambda}=\frac{2\pi.1,5}{6}=\frac{\pi}{2}\)

+ Phần tử sóng tại O dao động sớm pha hơn phần tử sóng tại M. Phương trình sóng tại O là:
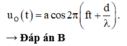

+ Điểm O gần nguồn sóng hơn, do đó sẽ dao động sớm pha so với phần tử môi trường tại :
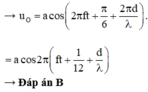

Đáp án B
+ Điểm O dao động sớm pha hơn M, với phương trình
u o = a cos 2 π f t + 1 12 + d λ

Ta có: \(\pi x=\frac{2\pi x}{\lambda}\Rightarrow\lambda=2m.\)
MN cách nhau 5m = 2,5 \(\lambda\) nên M, N dao động ngược pha.
Như vậy khi M qua VTCB theo chiều dương thì N qua VTCB theo chiều âm.

Từ "gần nhau nhất" ở câu a là thừa, vì 2 điểm đã lệch pha nhau \(\frac{\pi}{2}\) rồi.
Độ lệch pha của 2 điểm trên phương truyền sóng: \(\Delta\varphi=\frac{2\pi d}{\lambda}=\frac{\pi}{2}\)
Suy ra: \(d=\frac{\lambda}{4}\Rightarrow\lambda=4.d=4.5=20cm.\) \(\Rightarrow f=\frac{v}{\lambda}=\frac{20}{20}=1Hz\)
b) Vì sóng từ M đến O rồi đến N nên M sớm pha hơn O, N trễ pha hơn O.
\(u_M=4\sin\left(2\pi t-\frac{\pi}{6}+\frac{2\pi.50}{20}\right)=4\sin\left(2\pi t+\frac{29\pi}{6}\right)cm\)
\(u_N=4\sin\left(2\pi t-\frac{\pi}{6}-\frac{2\pi.50}{20}\right)=4\sin\left(2\pi t-\frac{31\pi}{6}\right)cm\)
không phải dmin bạn nhé.