
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có \(\frac{a^3}{b}+ab\ge2a^2\)
do đó VT +(ab + bc + ca) \(\ge2a^2+2b^2+2c^2\)
hay VT \(\ge2a^2+2b^2+2c^2-\left(ab+bc+ca\right)\ge a^2+b^2+c^2\) (đpcm).

\(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\) \(\ge\frac{3}{2}\)
\(\Leftrightarrow\frac{a}{b+c}+1+\frac{b}{a+c}+1+\frac{c}{a+b}+1\ge\frac{9}{2}\)
\(\Leftrightarrow\frac{a+b+c}{b+c}+\frac{a+b+c}{a+c}+\frac{a+b+c}{a+b}\ge\frac{9}{2}\)
\(\Leftrightarrow\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge\frac{9}{2}\)
\(\Leftrightarrow2\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge9\)
thật vậy\(2\left(a+b+c\right)\left(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{a+c}\right)\) =\(\left[\left(b+c\right)+\left(a+c\right)+\left(a+b\right)\right]\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge9\) (ÁP DỤNG BẤT ĐẲNG THỨC COSI)
ĐẲNG THỨC CUỐI ĐÚNG SUY RA ĐẲNG THỨC ĐẦU ĐƯỢC CHỨNG MINH


Bài 3:
a: Ta có: B và D đối xứng nhau qua AC
nên AC là đường trung trực của BD
Suy ra: CB=CD và AB=AD
Xét ΔCBA và ΔCDA có
CB=CD
BA=DA
CA chung
Do đó: ΔCBA=ΔCDA
Suy ra: \(\widehat{CBA}=\widehat{CDA}\)
mà \(\widehat{CBA}=90^0\)
nên \(\widehat{CDA}=90^0\)
Xét tứ giác ABCD có
\(\widehat{CBA}+\widehat{CDA}=180^0\)
nên ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc một đường tròn
b: Bán kính là \(\dfrac{CA}{2}\)

\(c,\left\{{}\begin{matrix}-4x+ay=1+a\\\left(6+a\right)x+2y=3+b\end{matrix}\right.\)
Để hpt có nghiệm duy nhất \(\Leftrightarrow\dfrac{-4}{6+a}\ne\dfrac{a}{2}\Leftrightarrow a^2+6a+8\ne0\Leftrightarrow\left\{{}\begin{matrix}a\ne-2\\a\ne-4\end{matrix}\right.\)
Để hpt vô nghiệm \(\Leftrightarrow\dfrac{-4}{6+a}=\dfrac{a}{2}\ne\dfrac{1+a}{3+b}\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-4}{6+a}=\dfrac{a}{2}\\\dfrac{a}{2}\ne\dfrac{1+a}{3+b}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}a=-2\\a=-4\end{matrix}\right.\\2+2a\ne3a+ab\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}a=-2\\a=-4\end{matrix}\right.\\a\ne2-ab\end{matrix}\right.\)
Để hpt có vô số nghiệm \(\Leftrightarrow\dfrac{-4}{6+a}=\dfrac{a}{2}=\dfrac{1+a}{3+b}\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-4}{6+a}=\dfrac{a}{2}\\\dfrac{a}{2}=\dfrac{1+a}{3+b}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}a=-2\\a=-4\end{matrix}\right.\\2+2a=3a+ab\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}a=-2\\a=-4\end{matrix}\right.\\a=2-ab\end{matrix}\right.\)


\(a,\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{\sqrt{x}}{\sqrt{x}+2}-\dfrac{2x}{x-4}\left(ĐKXĐ:x\ge0;x\ne4\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{2x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+3\sqrt{x}+2+x-2\sqrt{x}-2x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{1}{\sqrt{x}-2}\)
\(b,\dfrac{\sqrt{x}-2}{\sqrt{x}+1}-\dfrac{\sqrt{x}+3}{\sqrt{x}-1}-\dfrac{5\sqrt{x}+3}{1-x}\left(ĐKXĐ:x\ge0;x\ne1\right)\)
\(=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{5\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-3\sqrt{x}+2-\left(x+4\sqrt{x}+3\right)+5\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-3\sqrt{x}+2-x-4\sqrt{x}-3+5\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-2\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-2}{\sqrt{x}+1}\)
#\(Toru\)





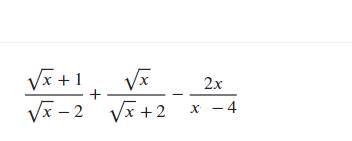
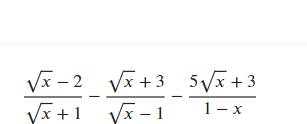
\(A\ge1\Leftrightarrow\dfrac{2\sqrt{x}-1}{\sqrt{x}-1}-1\ge0\\ \Leftrightarrow\dfrac{2\sqrt{x}-1-\sqrt{x}+1}{\sqrt{x}-1}\ge0\\ \Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-1}\ge0\\ \Leftrightarrow\sqrt{x}-1>0\left(\sqrt{x}\ge0\right)\\ \Leftrightarrow\sqrt{x}>1\Leftrightarrow x>1\)