Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số vở 7A,7B,7C ll là a,b,c(quyển;a,b,c∈N*)
Áp dụng tc dstbn:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+c}{2+4}=\dfrac{120}{8}=15\\ \Rightarrow\left\{{}\begin{matrix}a=30\\b=45\\c=60\end{matrix}\right.\)
Vậy ...

\(B=\left|x+1\right|+\left|x-4\right|+\left|2x-5\right|\ge\left|2x-3\right|+\left|2x-5\right|=\left|2x-3\right|+\left|5-2x\right|\)
\(\ge\left|2x-3+5-2x\right|=\left|2\right|=2\)
Dấu ''='' xảy ra khi \(\left(x+1\right)\left(4-x\right)\ge0;\left(2x-3\right)\left(5-2x\right)\ge0\)
\(-1\le x\le4;\frac{3}{2}\le x\le\frac{5}{2}\Rightarrow-1\le x\le4\)
Vậy GTNN của B bằng 2 tại -1 =< x =< 4

Các số được điền vào các ô theo thứ tự từ trái sang phải là:
-1; - \(\dfrac{1}{3}\); \(\dfrac{2}{3}\); \(\dfrac{4}{3}\)

https://hoc24.vn/cau-hoi/minh-can-rat-rat-gap-loi-giai-chi-tiet-2-phan-nay-de-bai-la-tinh-gtnn-moi-ng-giup-minh-voiiiiiiiiiiiiiiiiiiiii-ak-minh-cam-on.1527826665808
Mình làm ở đây rồi bạn nhé. Bạn vào link này tham khảo.

a. Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$|x-1|+|x-4|=|x-1|+|4-x|\geq |x-1+4-x|=3$
$|x-2|+|x-4|=|x-2|+|4-x|\geq |x-2+4-x|=2$
$|x-4|\geq 0$
Cộng theo vế:
$A\geq 5$
Vậy $A_{\min}=5$. Giá trị này đạt tại \(\left\{\begin{matrix} (x-1)(4-x)\geq 0\\ (x-2)(4-x)\geq 0\\ x-4=0\end{matrix}\right.\Leftrightarrow x=4\)
c. Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ thì:
$|x-3|+|x-8|=|x-3|+|8-x|\geq |x-3+8-x|=5$
$|x-5|+|x-8|=|x-5|+|8-x|\geq |x-5+8-x|=3$
$3|x-8|\geq 0$
Cộng theo vế:
$C\geq 8$. Vậy $C_{\min}=8$. Giá trị này đạt tại $x=8$


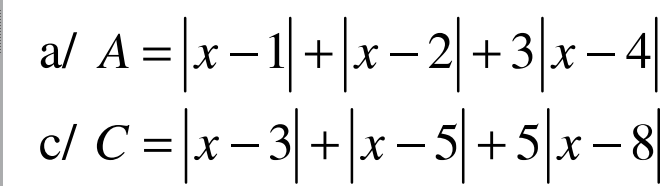
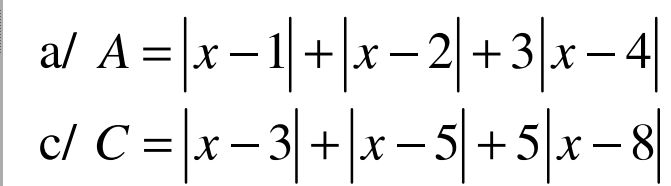
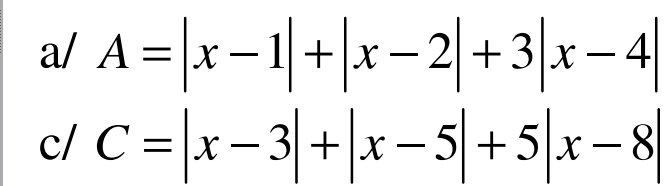
a/ Ta có: \(\begin{matrix}a\text{ // }b\\a\perp AB\end{matrix}\Rightarrow b\perp AB\)
b/ \(\hat{ACD}+\hat{CDB}=180^o\) (trong cùng phía, a // b)
\(\Rightarrow\hat{CDB}=180^o-\hat{ACD}=60^o\)
\(\hat{ACD}+\hat{aCD}=180^o\) (kề bù)
\(\Rightarrow\hat{aCD}=180^o-\hat{ACD}=60^o\)