Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(Z_L=140\Omega\)
\(Z_L=100\Omega\)
R thay đổi để P mạch cực đại khi \(R+r=\left|Z_L-Z_C\right|\Leftrightarrow R+30=\left|140-100\right|\Leftrightarrow R=10\Omega\)
Bonus: \(P_{max}=\frac{U^2}{2\left(R+r\right)}=\frac{100^2}{2\left(10+30\right)}=125W\)

R1 + R2 = U2/P => U=120 V
R1R2 =(ZL-ZC)2=5184
Cos$1 = R1/(R12+R1R2)0.5=0.6
Cos$2=R2/(R22+R1R2)0.5=0.8

\(Z_L=\omega L=140\Omega\)
\(Z_C=\dfrac{1}{\omega C}=100\Omega\)
Công suất của cuộn dây: \(P_{cd}=I^2.r=\dfrac{U^2}{(R+r)^2+(Z_L-Z_C)^2}.30=\dfrac{100^2}{(R+30)^2+(140-100)^2}.30\)
Từ biểu thức trên ta thấy \(P_{cdmax}\) khi \(R=0\)
Lúc đó \(P_{cdmax}=\dfrac{100^2}{30^2+40^2}.30=120W\)

\(Z_L=\omega L=140\Omega\)
\(Z_C=\dfrac{1}{\omega C}=100\Omega\)
R thay đổi để công suất tiêu thụ trên biến trở R cực đại khi
\(R=Z_{đoạn-còn-lại}=\sqrt{r^2+(Z_L-Z_C)^2}=50\Omega\)
Công suất: \(P_{max}=\dfrac{U^2}{2(R+r)}=\dfrac{100^2}{2(30+50)}=62,5W\)

Một tụ điện có dung kháng 30ΩΩ. chọn cách ghép tụi điện này nối tiếp với các linh kiện điện tử khác dưới đây để được một đoạn mạch mà dòng điện qua nó trễ pha so với hiệu điện thế 1 góc π4π4? tụ ghép với một:
A: cuộn thuần cảm có cảm kháng = 60 Ω
B: điện trở thuần có độ lớn 30 Ω
C: điện trở thuần có độ lớn 15 Ωvà cuộn dây thuần cảm có độ cảm kháng 15 ΩΩ
D : Điện thuần có độ lớn 30 Ω và cuộn dây thuần cảm có độ cảm kháng 60 Ω
Ω ΩΩ
Câu này \(C=\frac{10^{-3}}{4\pi}F\) mới ra ạ
\(\Rightarrow Z_L=100\Omega ; Z_C=40\Omega\)
\(P=\frac{U^2.R}{R^2+\left(Z_L-Z_C\right)^2}=45\)\(\Leftrightarrow\frac{75^2.R}{R^2+60^2}=45 \Leftrightarrow 75^2R=45R^2+45.60^2\)
\(\Leftrightarrow R=80\Omega\) hoặc\(R=20\Omega\)
Câu D
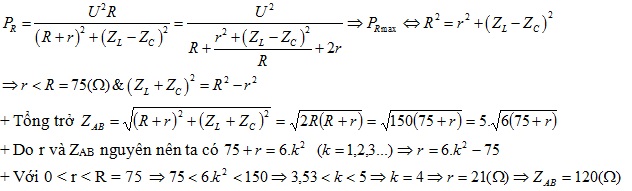
Công suất tiêu thụ của biến trở:
$P_R=\frac{U^2R}{(R+r)^2+(Z_L-Z_C)^2}=\frac{U^2}{R+\frac{r^2+(Z_L-Z_C)^2}{R}+2r}\leq \frac{U^2}{2\sqrt{r^2+(Z_L-Z_C)^2}+2r}$
Do đó, $P_R$ đạt giá trị lớn nhất khi $R=\sqrt{(Z_L-Z_c)^2+r^2}\Leftrightarrow Z_{AB}^2=75^2+(75+r)^2-r^2$
Giờ chỉ cần thử các giá trị nguyên ta thu được $r=21\Omega$ và $Z_{AB}=120\Omega$, tức đáp án $B$ là đáp án đúng.