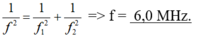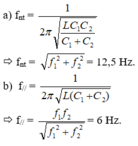Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tần số: \(f=\dfrac{1}{2\pi\sqrt {LC}}\Rightarrow f^2=\dfrac{a}{C}\) (a là 1 hằng số nào đó, do bài này f chỉ phụ thuộc vào C)
\(\Rightarrow f_1^2=\dfrac{a}{C_1}\)
\(f_2^2=\dfrac{a}{C_2}\)
Cần tìm: \(\Rightarrow f^2=\dfrac{a}{C}=a.(\dfrac{1}{C_1}+\dfrac{1}{C_2})=f_1^2+f_2^2\)
\(\Rightarrow f=\sqrt{30^2+40^2}=50(Hz)\)

Khi C thay đổi mà I không đổi → ZL=\(\frac{ZC1+ZC2}{2}\) → Zc2=20 → C2= \(\frac{5.10^{-4}}{\Pi}\)
\(\frac{5.10^{-4}}{\Pi}=\frac{10^{-3}}{2\Pi}\) haha ,đi thi mà cho kiểu đáp án lừa nhau thế thì cg vui đấy ..

Đáp án A
Phương pháp: Sử dụng công thức tính tần số của mạch dao động và công thức tụ mắc nối tiếp.
Cách giải:Công thức tính tần số mạch dao động là:
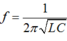
Công thức tính điện dung của tụ mắc nối tiếp là:
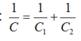
![]()
![]()