Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Sử dụng̣ vòng tròn lượng giác
Cách giải:
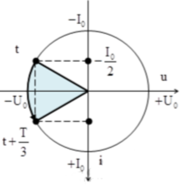
+ Trong quá trình dao động của mạch LC thì dòng điện luôn sớm pha π 3
so với điện áp hai đầu đoạn mạch
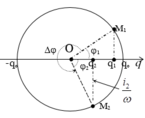
+ Phương pháp đường tròn
Từ hình vẽ ta thấy rằng sau khoảng thời gian T 3
điện áp giữa hai đầu tụ điện là - 3 2 U o và đang tăng

Bài này khá quen thuộc rồi. Giải như sau:
Đặt $q_1=Q_0\cos(\omega t_1)\Rightarrow i_1=Q_0\omega\cos(\omega t_1+\frac{\pi}{2})$
Sau $\frac{3T}{4}$: $i_2=Q_0\omega\cos\left ( \omega(t_1+\frac{3T}{4})+\frac{\pi}{2} \right )=Q_0\omega\cos (\omega t_1)$. $(1)$ Mà $i_1=-Q_0\omega\sin (\omega t_1)$
$\Rightarrow i_1^2+i_2^2=I_0^2$ $(\star)$
Áp dụng định luật bảo toàn năng lượng: $Li_2^2+\frac{q_2^2}{C}=LI_0^2$ $(\star \star)$
Từ $(\star), (\star \star)\Rightarrow q_2^2=LCi_1^2=\frac{i_1^2}{\omega ^2}\Rightarrow \omega=4.10^6\pi\rightarrow T=\frac{2\pi}{\omega}=5.10^7=0,5\mu s$
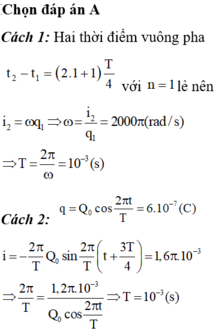


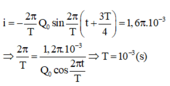
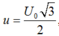

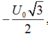
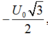

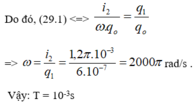

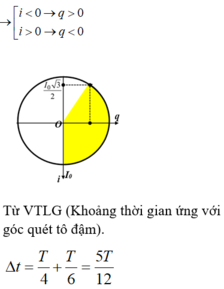
Giả sử điện tích của tụ là: \(q=Q_0\cos(\omega t)\)
Dòng điện có biểu thức là: \(i=q'=-\omega Q_0\sin(\omega t)=\omega Q_0\cos(\omega t+\dfrac{\pi}{2})\)
Thời điểm t: \(q=Q_0\cos(\omega t)=4,8.10^{-6}\)(1)
Sau T/4 ta có: \(i=\omega Q_0\cos(\omega (t+\dfrac{T}{4})+\dfrac{\pi}{2})=\omega Q_0\cos(\omega t+\pi)=-\omega Q_0\cos(\omega t)=2,4.10^{-3}\)(2)
Lấy (2) chia (1) vế với vế ta đc:
\(\omega =500\) (rad/s)
\(\Rightarrow T = \dfrac{2\pi}{500}=4\pi.10^{-3}s\)
Chọn D.
mk ko hỉu đề bn ơi