Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Quãng đường xe khách đi được sau \(x\) giờ với vận tốc 40 km/h là \(40.x\) (km)
Vì ban đầu bến xe cách bưu điện Nha Trang 6 km nên sau \(x\) giờ xe khách cách bưu điện thành phố Nha Trang số km là: \(40x + 6\). Do đó, \(y = 40x + 6\) với \(y\) là số km xe khách cách bưu điện thành phố Nha Trang sau \(x\) giờ.
b) Vì hàm số \(y = 40x + 6\) có dạng \(y = ax + b\) với \(a = 40;b = 6\) nên \(y\) là một hàm số bậc nhất theo biến \(x\).
c)
- Với \(x = 0 \Rightarrow y = f\left( 0 \right) = 40.0 + 6 = 6\);
- Với \(x = 1 \Rightarrow y = f\left( 1 \right) = 40.1 + 6 = 46\);
- Với \(x = 2 \Rightarrow y = f\left( 2 \right) = 40.2 + 6 = 86\);
- Với \(x = 3 \Rightarrow y = f\left( 3 \right) = 40.3 + 6 = 126\);
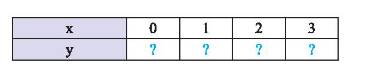
Ta có bảng sau:
\(x\) | 0 | 1 | 2 | 3 |
\(y\) | 6 | 46 | 86 | 126 |
Bảng này thể hiện khoảng cách của xe khách so với bưu điện Nha Trang sau 0 giờ; 1 giờ; 2 giờ; 3 giờ.

Quãng đường xe khách đi được sau \(x\) giờ với vận tốc 50 \(km/h\) là \(50.x\) (km)
Vì ban đầu bến xe cách bưu điện thành phố Huế 4 \(km\) nên sau \(x\) giờ xe khách cách bưu điện thành phố Huế số \(km\) là: \(50x + 4\). Do đó, \(y = 50x + 4\) với \(y\) là số \(km\) xe khách cách bưu điện thành phố Huế sau \(x\) giờ.

đề có sai không bạn? muốn đến sớm hơn mà lại đi với vận tốc nhỏ hơn (16km/h < 20km/h)?

Đáp án D
Gọi thời gian phải tìm là x (Phút)
Gọi thời gian Khiêm đi từ nhà đến trường là a (Phút)
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng ngược lại là: a/10
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng cùng chiều là: a/x
Số xe đi qua Khiêm khi Khiêm đi từ nhà đến trường cũng chính là số xe đã đi trên đoạn đường từ nhà Khiêm đến trường theo cả 2 chiều là: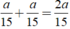
Ta có phương trình: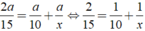
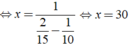
Vậy cứ sau 30 phút lại có xe cùng chiều vượt qua Khiêm.

Gọi thời gian phải tìm là x (Phút)
Gọi thời gian Khiêm đi từ nhà đến trường là a (Phút)
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng ngược lại là: a/10
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng cùng chiều là: a/x
Số xe đi qua Khiêm khi Khiêm đi từ nhà đến trường cũng chính là số xe đã đi trên đoạn đường từ nhà Khiêm đến trường theo cả 2 chiều là: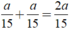
Ta có phương trình: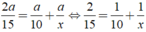
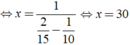
Vậy cứ sau 30 phút lại có xe cùng chiều vượt qua Khiêm.
Chọn đáp án C.

Hướng dẫn:
Gọi thời gian phải tìm là x (Phút)
Gọi thời gian Khiêm đi từ nhà đến trường là a (Phút)
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng ngược lại là: a/10
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng cùng chiều là: a/x
Số xe đi qua Khiêm khi Khiêm đi từ nhà đến trường cũng chính là số xe đã đi trên đoạn đường từ nhà Khiêm đến trường theo cả 2 chiều là: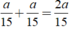
Ta có phương trình: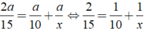
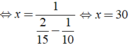
Vậy cứ sau 30 phút lại có xe cùng chiều vượt qua Khiêm.

Game này ez thôi bạn :))
Bài 1:
\(t_1=\frac{AB}{v_1}=\frac{AB}{15}\)
\(t_2=\frac{AB}{v_2}=\frac{AB}{30}\)
\(t=t_1-t_2\)
\(t=\frac{AB}{15}-\frac{AB}{30}\left(1\right)\)
\(t_1'=\frac{AB+10}{v_1}=\frac{AB+10}{15}\)
\(t_2'=\frac{\frac{AB}{2}}{v_2}+\frac{\frac{AB}{2}+10}{v_2-3}=\frac{\frac{AB}{2}}{30}+\frac{\frac{AB}{2}+10}{30-3}=\frac{AB}{2.30}+\frac{\frac{AB}{2}+10}{27}\)
\(t=t_1'-t_2'\)
\(t=\frac{AB+10}{15}-\frac{AB}{2.30}-\frac{\frac{AB}{2}+10}{27}\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\Rightarrow\frac{AB}{15}-\frac{AB}{30}=\frac{AB+10}{15}-\frac{AB}{2.30}-\frac{\frac{AB}{2}+10}{27}\)
\(\Rightarrow AB=560km\)
Bài 2:
\(t_1=\frac{AB}{v+3}\)
\(t=t_1+1\left(1\right)\)
\(t_2=\frac{AB}{v-2}\)
\(t=t_2-1\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\Rightarrow t_1+1=t_2-1\)
\(\frac{AB}{v+3}+2=\frac{AB}{v-2}\)
Vậy .......................................


Gọi quãng đường từ nhà tới bưu điện là s.
Nếu đi bộ, Long sẽ mất 1 khoảng thời gian =\(\frac{S}{5}\) (giờ).
Nếu đứng đợi và đi xe bus thì Long sẽ mất = 1/3 + s/30 (giờ)
Tức là nếu giả sử thời gian đi bộ = thời gian chờ + đi xe bus thì
s/5 = 1/3 + s/30
s/6 = 1/3
s = 2 (km).
Như vậy nếu quãng đường = 2 km, Long có thể đi bằng bất cứ cách nào cũng bằng nhau. Còn nếu quãng đừng lớn hơn > 2 km, lúc đó cứ lấy đại 1 giá trị lớn hơn 2 (giả sử s = 30 km) thế vào 2 biểu thức trên. Lúc đó, đi xe bus sẽ nhanh hơn.
Tương tự cho trường hợp quãng đường nhỏ hơn 2 km, đi bộ sẽ là giả pháp tốt hơn.
1/ bưu điện kế nhà long
kết quả => đi bộ
2/ bưu điện rất xa hoặc trung bình
ta có là tốc độ xe buýt 20km / h = 0.33333 km/phút
ta có tốc độ xe 2 chân 5km/h = 0.08333 km/phút
thời gian để xe buýt dí kịp xe 2 chân là
0.08333*20 = 1.6666 km
quãng đường xe = quãng đường 2 chân +1.666
thời gian = t
t(0.33333) = t(0.08333) +1.6666
=>t = 6.6664
vậy sau khi lên xe buýt 6.6664 phút thì dí kịp