Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Số trung bình: \(\overline x = \frac{{0.10 + 1.30 + 2.40 + 3.20}}{{100}} = 1,7\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm, \(\underbrace {0,...,0}_{10},\underbrace {1,...,1}_{30},\underbrace {2,...,2}_{40},\underbrace {3,...,3}_{20}.\)
Bước 2: Vì \(n = 100\), là số chẵn nên \({Q_2} = \frac{1}{2}(2 + 2) = 2\)
\({Q_1}\) là trung vị của nửa số liệu: \(\underbrace {0,...,0}_{10},\underbrace {1,...,1}_{30},\underbrace {2,...,2}_{10}.\) Do đó \({Q_1} = \frac{1}{2}(1 + 1) = 1\)
\({Q_3}\) là trung vị của nửa số liệu \(\underbrace {2,...,2}_{30},\underbrace {3,...,3}_{20}.\) Do đó \({Q_3} = \frac{1}{2}(2 + 2) = 2\)
+) Mốt \({M_o} = 2\)

Tổng số khả năng có thể xảy ra của phép thử là \(n\left( \Omega \right) = C_{13}^2.13\)
a) Biến cố “Ba quả bóng lấy ra cùng màu” xảy ra khi hai lần đều lấy ra bóng có cùng màu xanh, đỏ hoặc vàng. Số kết quả thuận lợi cho biến cố là \(C_5^2.5 + C_6^2.6 + C_2^2.2 = 142\)
Vậy xác suất của biến cố “Ba quả bóng lấy ra cùng màu” là \(P = \frac{{142}}{{13C_{13}^2}} = \frac{{71}}{{507}}\)
b) Số kết quả thuận lợi cho biến cố “Bóng lấy ra lần 2 là bóng xanh” là \(C_{13}^2.5\)
Vậy xác suất của biến cố “Bóng lấy ra lần 2 là bóng xanh” là \(P = \frac{{5C_{13}^2}}{{13C_{13}^2}} = \frac{5}{{13}}\)
c) Biến cố “Ba bóng lấy ra có ba màu khác nhau” xảy ra khi hai quả bóng lấy ra lần đầu là 2 màu khác nhau và quả bóng lấy lần 2 có màu còn lại. Số kết quả thuận lợi cho biến cố này là \(5.6.2.3 = 180\)
Vậy xác suất của biến cố “Ba bóng lấy ra có ba màu khác nhau” là \(P = \frac{{180}}{{13C_{13}^2}} = \frac{{30}}{{169}}\)
Cái này nhân 3 TH thui
VD (xanh+đỏ; vàng) ; (xanh+vàng; đỏ); (đỏ+vàng;xanh) nên x3 chứ không phải nhân 3! á em (câu c)

Ta thấy hai biến cố :”Hai quả bóng lây ra cùng màu” và “Hai quả bóng lấy ra khác màu” là hai biến cố đối
Suy ra xác suất của biến cố “Hai quả bóng lây ra cùng màu” là \(1 - 0,6 = 0,4\)

a) Lần đầu tiên lấy thẻ, sau đó để lại vào hộp nên lần thứ 2 cũng sẽ có 3 trường hợp với 3 số xảy ra, nên ta có không gian mẫu của phép thử là:
\(\Omega = \left\{ {\left( {i;j} \right)\left| {i,j = 1,2,3} \right.} \right\}\) với i, j lần lượt là số được đánh trên thẻ được lấy lần đầu và lần hai
b) Lần đầu lấy một thẻ từ hộp, xem số, bỏ ra ngoài rồi lấy tiếp 1 thẻ khác từ hộp, nên lần hai chỉ có 2 trường hợp với hai số còn lại, nên ta có không gian mẫu của phép thử là:
\(\Omega = \left\{ {(1;2),(1;3),(2;1),(2;3),(3;1),(3;2)} \right\}\)
(Với kết quả của phép thử là cặp số (i; j) trong đó i và j lần lượt là số được đánh trên thẻ được lấy ra lần thứ nhất và thứ hai)
c) Ta lấy đồng thời hai thẻ nên các số được đánh trên thẻ là khác nhau
\(\Omega = \left\{ {(1;2),(1;3),(2;1),(2;3),(3;1),(3;2)} \right\}\)
(Với kết quả của phép thử là cặp số (i; j) trong đó i và j lần lượt là số được đánh trên thẻ được lấy ra lần thứ nhất và thứ hai)

`\Omega_1=C_9 ^1=9`
`\Omega_2=C_13 ^2=78`
`@TH1:`
Gọi `A:`"Lấy từ hộp thứ nhất viên bi trắng."
`=>A=C_5 ^1=5`
`=>P(A)=5/9`
Gọi `B:`" Lấy từ hộp thứ hai `2` viên bi trắng."
`=>B=C_8 ^2=28`
`=>P(B)=5/9 . 28/78=70/351`
`@TH2:`
Gọi `C:`"Lấy từ hộp thứ nhất viên bi xanh."
`=>C=C_4 ^1=4`
`=>P(C)=4/9`
Gọi `D:`" Lấy từ hộp thứ hai `2` viên bi trắng."
`=>D=C_7 ^2=21`
`=>P(D)=4/9 . 21/78=14/117`

Gọi A là biến cố “Không bạn nào lấy đúng thẻ của mình”
Các kết quả có thể xảy ra khi các bạn lần lượt lấy thẻ được thể hiện ở sơ đồ hình cây như hình dưới
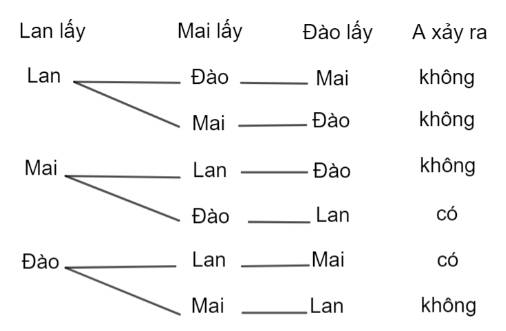
Có tất cả 6 kết quả có thể xảy ra, trong đó có 2 kết quả thuận lợi cho A, do đó:
\(P\left( A \right) = \frac{2}{6} = \frac{1}{3}\)


Chia 16 số ra làm 3 tập:
A={1;4;7;10;13;16}; B={2;5;8;11;14}; C={3;6;9;12;15}
TH1: 1 số trong A, 1 số trong B, 1 số trong C
=>Có 6*5*5=150 cách
TH2: 3 số trong A
=>Có \(C^3_6=20\left(cách\right)\)
TH3: 3 số trong B hoặc C
=>Có \(C^3_5\cdot2=20\left(cách\right)\)
=>n(A)=20+20+150=190
\(n\left(omega\right)=C^3_{16}=560\)
=>P(A)=19/56

Do lần đầu tiên lấy bóng sau đó trả lại hộp nên lần hai có thể lấy 1 trong 4 quả bóng và hai lần lấy lần lượt nên ta cần phải tính đến thứ tự lấy bóng. Nếu lần đầu lấy được bóng 1 và lần hai lấy được bóng 3 thì ta sẽ kí hiệu kết quả của phép thử là cặp (1; 3). Khi đó không gian mẫu của phép thử là:
\(\Omega = \left\{ \begin{array}{l}(1;1);(1;2);(1;3);(1;4);(2;1);(2;2);(2;3);(2;4);\\(3;1);(3;2);(3;3);(3;4);(4;1);(4;2);(4;3);(4;4)\end{array} \right\}\)