NV
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QT
1
23 tháng 9 2023
Tham khảo:
Tam thức bậc hai \(f\left( x \right) = - {x^2} - 2x + 8\) có hai nghiệm phân biệt \({x_1} = - 4,{x_2} = 2\) và hệ số \(a = - 1 < 0\).
Ta có bảng xét dấu \(f\left( x \right)\) như sau:
NT
11 tháng 4 2020
1. Ta có : 3x+12=0 <=> x= -4
bảng xét dấu:
| x | -∞ -4 + ∞ |
| 3x+12 |
- 0 + |
f(x) >0 ∀ x ∈ (-4;+∞)
f(x) <0 ∀ x∈ (-∞;-4)
2. Ta có : -5x+9=0 <=> x= \(\frac{9}{5}\)
Bảng xét dấu:
| x | -∞ 9/5 +∞ |
| -5x+9 | + 0 - |
f(x) >0 ∀ x ∈ (-∞; 9/5)
f(x) <0 ∀ x ∈(9/5; +∞)
3. Ta có : -3x-9=0 <=> x= -3
| x | -∞ -3 +∞ |
| -3x-9 | + 0 - |
f(x) >0 ∀ x∈ (-∞; -3)
f(x) <0 ∀x∈ ( -3; +∞ )
4. Ta có : x (2x+4)=0
+, x=0
+, 2x+4=0 <=> x= -2
| x | -∞ -2 0 +∞ |
| x | - \(|\) - 0 + |
| 2x+4 | - 0 + \(|\) + |
| f (x) | + 0 - 0 + |
f(x) >0 ∀ x ∈ (-∞; -2) \(\cup\) (0; +∞)
f(x) <0 ∀ x ∈ (-2;0)
5. Ta có: (x-2)(-x+4)=0
+, x-2=0 <=> x=2
+, -x+4=0 <=> x= 4
| x | -∞ 2 4 +∞ |
| x-2 | - 0 + \(|\) + |
| -x+4 | + \(|\) + 0 - |
| f(x) | - 0 + 0 - |
f(x) >0 ∀ x ∈ (2;4)
f (x) <0 ∀x∈ (-∞;2) \(\cup\)(4; +∞)
6. Ta có : (-4x+3)(x-6)=0
+, -4x+3=0 <=>x= \(\frac{3}{4}\)
+, x-6 =0 <=> x=6
| x | -∞ 3/4 6 +∞ |
| -4x+3 | + 0 - \(|\) - |
| x-6 | - \(|\) - 0 + |
| f(x) | - 0 + 0 - |
f(x) >0 ∀ x∈ (3/4;6)
f(x) <0 ∀ x∈ (-∞; 3/4) \(\cup\)(6;+∞)
23 tháng 9 2023
Tham khảo:
a) Ta có tam thức bậc hai \(f\left( x \right) = {x^2} - x - 2\) có 2 nghiệm phân biệt \({x_1} = - 1,{x_2} = 2\) và hệ số \(a = 1 > 0\)
Ta có bảng xét dấu f(x) như sau:
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right) \cup \left( {2; + \infty } \right)\)b) Từ bảng xét dấu ta thấy \(f\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}x < - 1\\x > 2\end{array} \right.\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 9 2019
a/ \(f\left(-x\right)=\left(-x\right)^2+3\left(-x\right)^4=x^2+3x^4=f\left(x\right)\)
Hàm chẵn
b/ \(f\left(-x\right)=\left(-x\right)^3+3\left(-x\right)=-x^3-3x=-\left(x^3+3x\right)=-f\left(x\right)\)
Hàm lẻ
c/ \(f\left(-x\right)=-2\left(-x\right)^4+\left(-x\right)^2-1=-2x^4+x^2-1=f\left(x\right)\)
Hàm chẵn
d/ \(f\left(1\right)=6\); \(f\left(-1\right)=-2\ne f\left(1\right)\ne-f\left(1\right)\)
Hàm ko chẵn ko lẻ
e/ Tương tự câu trên, hàm ko chẵn ko lẻ
f/ \(f\left(-x\right)=\frac{2\left(-x\right)^2-4}{-x}=\frac{2x^2-4}{-x}=-\left(\frac{2x^2-4}{x}\right)=-f\left(x\right)\)
Hàm lẻ trong miền xác định
23 tháng 9 2023
Tham khảo:
a) \(f\left( x \right) = - 3{x^2} + 4x - 1\)
\(a = - 3 < 0\), \(\Delta = {4^2} - 4.\left( { - 3} \right).\left( { - 1} \right) = 4 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = \frac{1}{3},x = 1\)
Bảng xét dấu:
b) \(f\left( x \right) = {x^2} - x - 12\)
\(a = 1 > 0\), \(\Delta = {\left( { - 1} \right)^2} - 4.1.\left( { - 12} \right) = 49 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = - 3,x = 4\)
Bảng xét dấu:
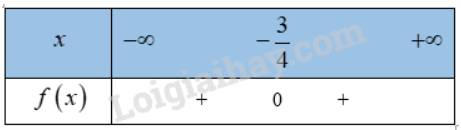
c) \(f\left( x \right) = 16{x^2} + 24x + 9\)
\(a = 16 > 0\), \(\Delta ' = {12^2} - 16.9 = 0\)
=> \(f\left( x \right)\) có nghiệm duy nhất \(x = - \frac{3}{4}\)
Bảng xét dấu:
TN
7 tháng 7 2019
a) \(\left(x-4\right)\left(x-5\right)\left(x-6\right)\left(x-7\right)=1680\\ \Leftrightarrow\left(x-4\right)\left(x-7\right)\left(x-5\right)\left(x-6\right)=1680\\ \Leftrightarrow\left(x^2-11x+28\right)\left(x^2-11x+30\right)=1680\\ \Leftrightarrow\left(x^2-11x+29-1\right)\left(x^2-11x+29+1\right)=1680\\ \)
Đặt \(x^2-11x+29=t\), ta đc \(\left(t-1\right)\left(t+1\right)=1680\\ \Leftrightarrow t^2-1=1680\Leftrightarrow t^2=1681\Leftrightarrow t=\pm41\)
Với \(t=41\Leftrightarrow x^2-11x+28=40\Leftrightarrow\left[{}\begin{matrix}x=12\\x=-1\end{matrix}\right.\)
Với \(t=-41\Leftrightarrow x^2-11x+30=-40\)(vô no)
Vậy.....
TN
7 tháng 7 2019
c) \(x^4-7x^3+14x^2-7x+1=0\\ \Leftrightarrow x^2-7x+14-\frac{7}{x}+\frac{1}{x^2}=0\)
\(\Leftrightarrow\left(x^2+\frac{1}{x^2}\right)-7\left(x+\frac{1}{x}\right)+14=0\)
Đặt \(x+\frac{1}{x}=t\Rightarrow x^2+\frac{1}{x^2}=t^2-2\)
Ta đc \(t^2-2-7t+14=0\Leftrightarrow t^2-7t+12=0\)
\(\Rightarrow\left[{}\begin{matrix}t=4\\t=3\end{matrix}\right.\)
B tự giải tiếp nha
17 tháng 11 2022
Câu 1:
a: =x^2+6x+9+4
=(x+3)^2+4>0
b: \(=x^2-4x+4+x^2+4xy+4y^2+9=\left(x-2\right)^2+\left(x+2y\right)^2+9>=9\)
Dấu = xảy ra khi x=2 và y=-x/2=-2/2=-1
UK F(X) BAN G F(X)