Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nêu rõ các bước tính. Ý nghĩa của số trung bình cộng. Khi nào thì số trung bình cộng khó có thể là đại diện của dấu hiệu đó?
Để tính số trung bình cộng của các giá trị của dấu hiệu (nếu số đơn vị điều tra khá lớn) ta lập thêm trong bảng tần số một cột (dòng) ghi các tích mỗi giá trị nhân với tần số tương ứng của chúng.
- Tính tổng các số cột (dòng) tích
- Lấy tổng vừa tính được ở trên chia cho N.
Công thức tính số trung bình cộng:
Ý nghĩa: Số trung bình cộng thường được dùng làm "đại diện" cho dấu hiệu, đặc biệt là khi muốn so sánh các dấu hiệu cùng loại.
Nếu trong dãy các giá trị của dấu hiệu có những giá trị có khoảng cách chênh lệch khá lớn thì lấy số trung bình cộng làm giá trị đại diện cho dấu hiệu không có ý nghĩa thực tế
* Ta có thể tính số TBC của 1 dấu hiệu ( gọi tắt là số TBC của kí hiệu là \(\overline{X}\) ) như sau :
- Nhân từng giá trị với tần số tương ứng.
- Cộng tất cả các tích vừa tìm được
- Chia tổng đó cho số các giá trị ( tức tổng các tần số )
* Ý nghĩa : Số TBC thường đc dùng làm "đại diện" cho dấu hiệu, đặc điểm là khi muốn so sánh các dấu hiệu cùng loại.
Chú ý : Khi các giá trị của dấu hiệu có khoảng cách chênh lệch rất lớn đối với nhau thì ko nên lấy số TBC làm "đại diện" cho dấu hiệu.

Để tính số trung bình cộng của các giá trị của dấu hiệu (nếu số đơn vị điều tra khá lớn) ta lập thêm trong bảng tần số một cột (dòng) ghi các tích mỗi giá trị nhân với tần số tương ứng của chúng.
- Tính tổng các số cột (dòng) tích
- Lấy tổng vừa tính được ở trên chia cho N.
Công thức tính số trung bình cộng:
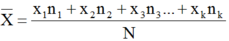 Trong đó:
Trong đó:
x1, x2, ..., xk là k giá trị khác nhau của dấu hiệu x
n1, n2, ..., nk là k tần số tương ứng
N là số các giá trị
Ý nghĩa: Số trung bình cộng thường được dùng làm "đại diện" cho dấu hiệu, đặc biệt là khi muốn so sánh các dấu hiệu cùng loại.
Nếu trong dãy các giá trị của dấu hiệu có những giá trị có khoảng cách chênh lệch khá lớn thì lấy số trung bình cộng làm giá trị đại diện cho dấu hiệu không có ý nghĩa thực tế.

Vấn đề là không hề dễ để vẻ được 1 tam giác đều trong cái pizza!
Để chia một hình tròn thành 3 phần bằng nhau thì đơn giản ta chỉ cần chia theo các góc 120 độ ở tâm là được.
Trước hết dùng sợi đây dài 4 cm căng 2 lần sao cho vừa chiếc bánh rồi lấy giao điểm 2 lần căng đó thì ta có tâm hình tròn.
Tiếp đến có thể dùng thước đo góc để do lấy góc 120 độ trên tờ giấy bự, sau đó cắt tờ giấy có góc 120 độ ra và ép lên miếng bánh sao cho đỉnh góc trùng với tâm hình tròn rồi cắt theo đường giới hạn của tờ giấy.
Làm 2 lần, ta được 3 phần bánh có hình dạng và kích thước như nhau!
Vẽ tam giác đều nội tiếp đường tròn (O;2cm) (cái bánh PIZZA ấy). Vẽ 3 đường trung tuyến của tam giác đó. Trong SGK, người ta đã chứng minh rằng khi tam giác thành 3 phần theo trung tuyến thì sẽ tạo ra 3 tam giác bằng nhau. Suy ra nếu cắt hình tròn (O;2cm) thành 3 phần theo trung tuyến của tam giác nội tiếp ấy cũng tạo ra 3 phần hình tròn bằng nhau, vì trọng tâm của tam giác nằm trùng với tâm đường tròn. Thế là giải ra! Khó lắm đúng không! Mình nằm cả buổi trưa để suy nghĩ.

Made -> Table là chuẩn không cần chỉnh
Ai mà ấn Đúng 0 sẽ được may mắn cả năm

\(\left(\frac{1}{7}\right)^7.7^7\)=\(\frac{1^7}{7^7}.7^7=1^7=1\)

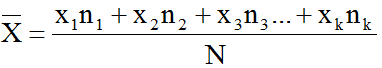
vào youtube gõ senioz xem linh