K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 2 2020
Để \(\frac{2x-4}{x+2}\)nguyên thì
\(2x-4⋮x+2\)
\(\Rightarrow2\left(x+2\right)-8⋮x+2\)
Mà \(2\left(x+2\right)⋮x+2\)
\(\Rightarrow8⋮x+2\)
\(\Rightarrow x+2\in\left\{1;2;4;8;-1;-2;-4;-8\right\}\)
\(\Rightarrow x\in\left\{-1;0;2;6;-3;-4;-6;-10\right\}\)
Học tốt
A
, mình đang cần giải gấp. Cảm ơn mn nhiều.
1
3 tháng 9 2021
Bài 3:
a: Gọi OK là khoảng cách từ O đến AB
Suy ra: K là trung điểm của AB
hay \(AK=BK=\dfrac{AB}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Áp dụng định lí Pytago vào ΔOKA vuông tại K, ta được:
\(OA^2=OK^2+KA^2\)
hay OK=3(cm)
A
0
A
1
26 tháng 9 2021
c: \(f\left(5-2\sqrt{3}\right)=f\left(2\right)\)
\(\Leftrightarrow\sqrt{4-2\sqrt{3}}+m\left(5-2\sqrt{3}\right)+2=\sqrt{2-1}+2m+2\)
\(\Leftrightarrow\sqrt{3}+1+m\left(5-2\sqrt{3}\right)=2m+3\)
\(\Leftrightarrow m\left(3-2\sqrt{3}\right)=2-\sqrt{3}\)
hay \(m=-\dfrac{\sqrt{3}}{3}\)
PA
1
17 tháng 7 2021
1) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
NP
1
9 tháng 7 2023
b: Gọi giao của AH với BC là F
=>AH vuông góc BC tại F
góic CHI=góc AHD=90 độ-góc HAD=góc ABC=1/2*sđ cung AC
góc CIH=1/2*sđ cung CA
=>góc CHI=góc CIH
=>ΔCHI cân tại C
c:
góc BDC=góc BEC=90 độ
=>BDEC nội tiếp đường tròn đường kính BC
=>MD=ME
=>ΔMDE cân tại M
mà MN là trung tuyến
nên MN vuông góc DE
Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC
=>góc xAC=góc AED
=>Ax//DE
=>DE vuông góc OA
=>MN//AO
NT
1
7 tháng 10 2021
a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CN là tiếp tuyến có N là tiếp điểm
Do đó: CM=CN
hay C nằm trên đường trung trực của MN(1)
Ta có: OM=ON
nên O nằm trên đường trung trực của MN(2)
Từ (1) và (2) suy ra OC là đường trung trực của MN
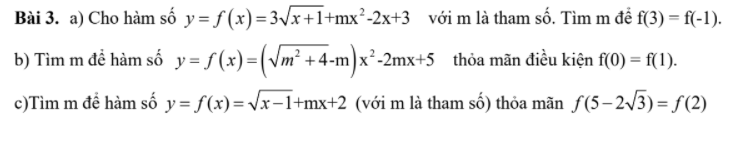
\(4x-9.3x-10.2x=0\)
\(=>4x-27x-20x=0\)
\(=>x\left(4-27-20\right)=0\)
\(=>x.\left(-43\right)=0\)
\(=>x=0\)