K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
D
datcoder
CTVVIP
14 tháng 10 2023
a)
\(175\cdot19+38\cdot175+43\cdot175\\ =175\cdot19+175\cdot38+175\cdot43\\ =175\cdot\left(19+38+43\right)\\ =175\cdot100\\ =17500\)
b)
\(125\cdot75+125\cdot13-80\cdot125\\ =125\cdot75+125\cdot13-125\cdot80\\ =125\cdot\left(75+13-80\right)\\ =125\cdot10\\ =125\cdot8\\ =1000\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 10 2023
a, 175. 19 + 38. 175 + 43. 175
= 175. 19 + 175. 38 + 175. 43
= 175.(19 + 38 + 43)
= 175. 100
= 17500
D
datcoder
CTVVIP
5 tháng 12 2023
2/
Xét phân số \(\dfrac{2n-3}{n+1}=\dfrac{2n+2-5}{n+1}=\dfrac{2n+2}{n+1}-\dfrac{5}{n+1}=\dfrac{2\left(n+1\right)}{n+1}-\dfrac{5}{n+1}=2-\dfrac{5}{n+1}\)
\(n\in Z\Rightarrow2n-3\inƯ\left(5\right)=\left\{-1;-5;1;5\right\}\)
Ta có bảng:
| 2n - 3 | -1 | -5 | 1 | 5 |
| n | 1 | -1 | 2 | 4 |
Vậy \(n\in\left\{-1;1;2;4\right\}\)
D
datcoder
CTVVIP
5 tháng 12 2023
1/
(x + 1) + (x + 3) + (x + 5) + ... + (x + 999) = 500
<=> (x + x + x + ... + x) + (1 + 3 + 5 + ... + 999) = 500
Xét tổng A = 1 + 3 + 5 + ... + 999
Số số hạng của A là: (999 - 1) : 2 + 1 = 500
Tổng A là: (999 + 1) x 500 : 2 = 250 000
Do A có 500 số hạng nên có 500 ẩn x.
Vậy ta có: 500x + 250 000 = 500
=> 500x = -249 500
=> x = 499
Vậy x = 499
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 1 2024
4.
\(\dfrac{x-7}{y-6}=\dfrac{7}{6}\Rightarrow\dfrac{x-7}{7}=\dfrac{y-6}{6}=\dfrac{-y+6}{-6}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{x-7}{7}=\dfrac{-y+6}{-6}=\dfrac{x-7-y+6}{7-6}=\dfrac{x-y-1}{1}=-5\)
\(\Rightarrow\left\{{}\begin{matrix}x-7=7.\left(-5\right)=-35\\-y+6=\left(-6\right).\left(-5\right)=30\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-28\\y=-24\end{matrix}\right.\)
5.
Ta có:
\(A^2=\dfrac{2^2.4^2.6^2...4998^2.5000^2}{3^2.5^2.7^2...4999^2.5001^2}< \dfrac{2^2.4^2.6^2.4998^2.5000^2}{\left(3^2-1\right)\left(5^2-1\right)\left(7^2-1\right)...\left(4999^2-1\right)\left(5001^2-1\right)}\)
\(\Rightarrow A^2< \dfrac{2^2.4^4.6^2...4998^2.5000^2}{2.4.4.6.6.8...4998.5000.5000.5002}=\dfrac{2^2.4^4.6^2...4998^2.5000^2}{2.4^4.6^2...4998^2.5000^2.5002}\)
\(\Rightarrow A^2< \dfrac{2}{5002}=\dfrac{1}{2501}< \dfrac{1}{2500}\)
\(\Rightarrow A< \dfrac{1}{50}\)
\(\Rightarrow A< 0,02\)
H9
HT.Phong (9A5)
CTVHS
14 tháng 1 2024
Bài 3:
\(A=B\) khi:
\(\dfrac{7}{y-2}=x+1\left(y\ne2\right)\)
\(\Rightarrow\left(x+1\right)\left(y-2\right)=7\)
Mà: x,y nguyên \(\Rightarrow x+1,y-2\inƯ\left(7\right)=\left\{1;-1;7;-7\right\}\)
Ta có bảng sau:
| x + 1 | 1 | -1 | 7 | -7 |
| y - 2 | 7 | -7 | 1 | -1 |
| x | 0 | -2 | 6 | -8 |
| y | 9 | -5 | 3 | 1 |
AH
Akai Haruma
Giáo viên
4 tháng 2 2024
Lời giải:
a.
$=\frac{3}{5}-\frac{7}{4}=\frac{12-35}{20}=\frac{-23}{20}$
b.
$=-(2+\frac{5}{8})=-\frac{21}{8}$
c.
$=-(\frac{1}{8}+\frac{5}{9})=-\frac{9+8.5}{8.9}=\frac{-49}{72}$
d.
$=\frac{6}{13}-\frac{14}{39}=\frac{18}{39}-\frac{14}{39}=\frac{4}{39}$
e.
$=\frac{-3}{4}+\frac{5}{7}=\frac{5}{7}-\frac{3}{4}$
$=\frac{20-21}{7.4}=\frac{-1}{28}$
KV
25 tháng 1 2024
Bài 5
1) x ∈ Ư(18) = {1; 2; 3; 6; 9; 18}
x ∈ B(4) = {0; 4; 8; 12; 16; 20; ...}
Vậy không tìm được x thỏa mãn đề bài
2) x ∈ Ư(20) = {1; 2; 4; 5; 10; 20}
x ∈ B(2) = {0; 2; 4; 6; 8; 10; 12; 14; 16; 18; 20; ...}
⇒ x ∈ {2; 4; 10; 20}
3) x ∈ B(12) = {0; 12; 24; 36; 48; ...; 96; 108; ...}
Mà 30 ≤ x ≤ 100
⇒ x ∈ {36; 48; ...; 96}
4) x ∈ Ư(150) = {1; 2; 3; 5; 6; 10; 15; 25; 30; 50; 75; 150}
Mà x ≤ 50
⇒ x ∈ {1; 2; 3; 5; 6; 10; 15; 25; 30; 50}
5) 70 ⋮ x và 168 ⋮ x
⇒ x ∈ ƯC(70; 168)
Ta có:
70 = 2.5.7
168 = 2³.3.7
⇒ ƯCLN(70; 168) = 2.7 = 14
⇒ x ∈ ƯC(70; 168) = Ư(14) = {1; 2; 7; 14}
Mà x > 10
⇒ x = 14
6) Ta có:
(1995 + 2005 + x) ⋮ 5
1995 ⋮ 5
2005 ⋮ 5
⇒ x ⋮ 5
⇒ x ∈ B(5) = {0; 5; 10; 15; 20; 25; 30; 35; 40; ...}
Mà 23 < x ≤ 35
⇒ x ∈ {25; 30; 35}
KV
25 tháng 1 2024
Bài 6
1) Do 17x2y chia hết cho 2 và 5 nên y = 0
⇒ Số đã cho có dạng: 17x20
Để 17x20 chia hết cho 3 thì (1 + 7 + x + 2 + 0) ⋮ 3
⇒ (10 + x) ⋮ 3
⇒ x ∈ {2; 5; 8}
Vậy x ∈ {2; 5; 8}; y = 0
2) Do 234xy chia hết cho 2 và 5 nên y = 0
⇒ Số đã cho có dạng: 234x0
Để 234x0 chia hết cho 9 thì (2 + 3 + 4 + x + 0) ⋮ 9
⇒ (9 + x) ⋮ 9
⇒ x ∈ {0; 9}
Vậy x ∈ {0; 9}; y = 0
3) Do 4x6y chia hết cho 2 và 5 nên y = 0
Mà x - y = 4
⇒ x = 4 + y
⇒ x = 4
Vậy x = 4; y = 0
4) Do 57x2y chia hết cho 5 nhưng không chia hết cho 2 nên y = 5
⇒ Số đã cho có dạng 57x25
Để 57x25 chia hết cho 9 thì (5 + 7 + x + 2 + 5) ⋮ 9
⇒ (19 + x) ⋮ 9
⇒ x = 8
Vậy x = 8; y = 5
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
15 tháng 1 2024
\(a,-\dfrac{5}{7}+1+\dfrac{30}{-7}\le x\le-\dfrac{1}{6}+\dfrac{1}{3}+\dfrac{5}{6}\\ \dfrac{-5+1.7-30}{7}\le x\le\dfrac{-1+1.2+5}{6}\\ -\dfrac{28}{7}\le x\le\dfrac{6}{6}\\ -4\le x\le1\\ Vậy:x\in\left\{-4;-3;-2;-1;0;1\right\}\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
15 tháng 1 2024
\(b,\dfrac{-8}{13}+\dfrac{7}{17}+\dfrac{21}{13}\le x\le-\dfrac{9}{14}+3+\dfrac{5}{-14}\\ \left(\dfrac{21}{13}-\dfrac{8}{13}\right)+\dfrac{7}{17}\le x\le\left(-\dfrac{9}{14}-\dfrac{5}{14}\right)+3\\ 1+\dfrac{7}{17}\le x\le-1+3\\ 1\dfrac{7}{17}\le x\le2\\ Vậy:x=2\)
AH
Akai Haruma
Giáo viên
15 tháng 1 2024
Lời giải:
$\frac{1}{50}> \frac{1}{100}$
$\frac{1}{51}> \frac{1}{100}$
.....
$\frac{1}{98}> \frac{1}{100}$
$\frac{1}{99}> \frac{1}{100}$
$\Rightarrow S> \underbrace{\frac{1}{100}+\frac{1}{100}+...+\frac{1}{100}}_{50}=\frac{1}{100}.50=\frac{1}{2}$
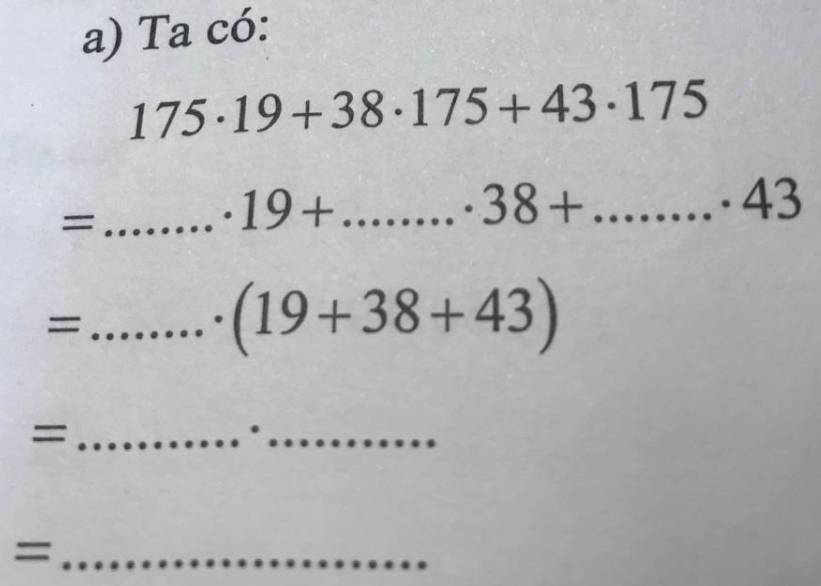
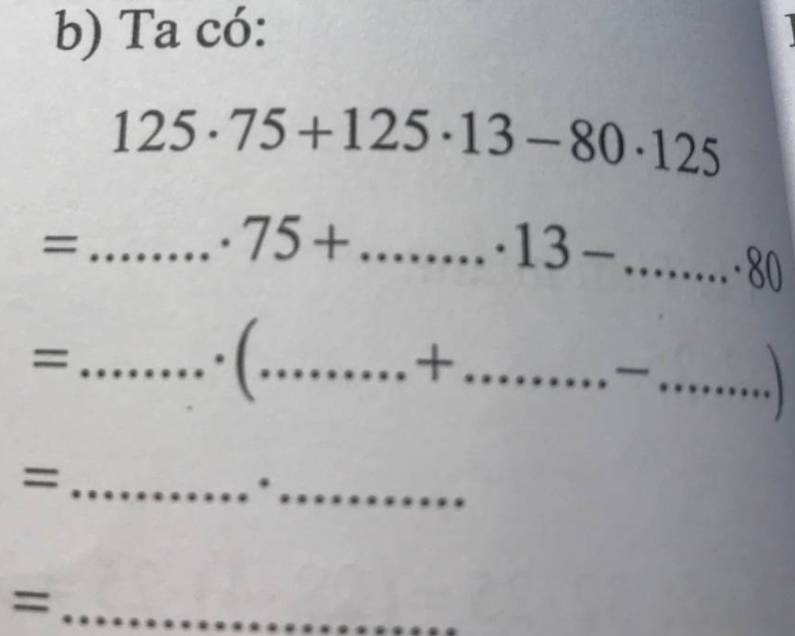
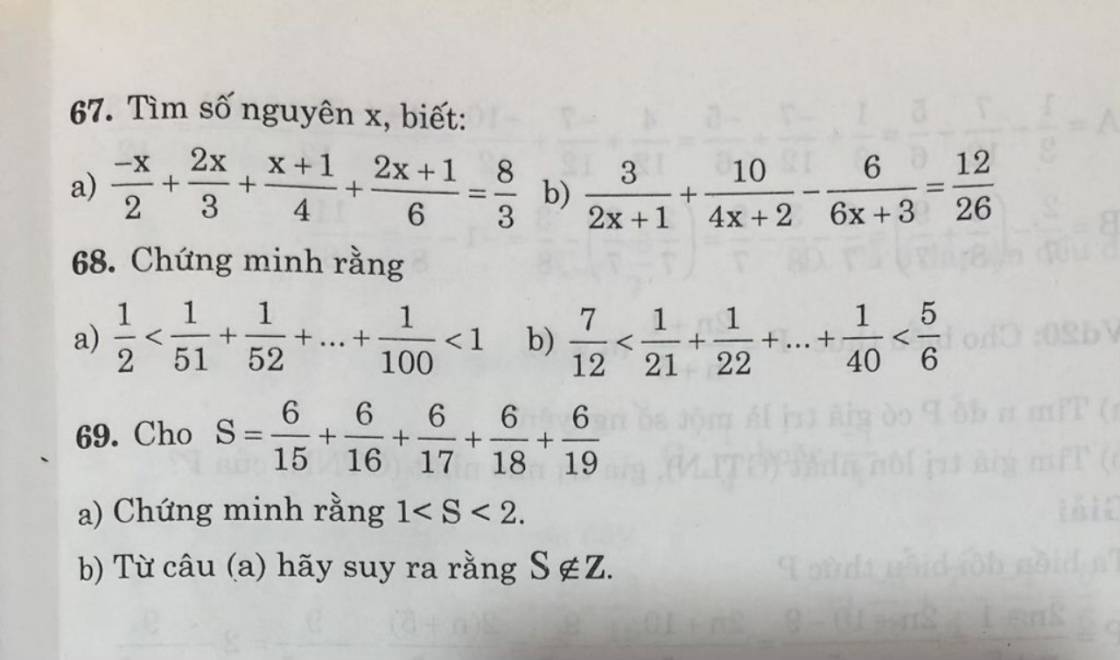
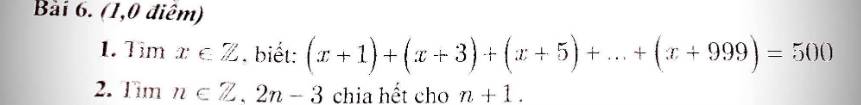
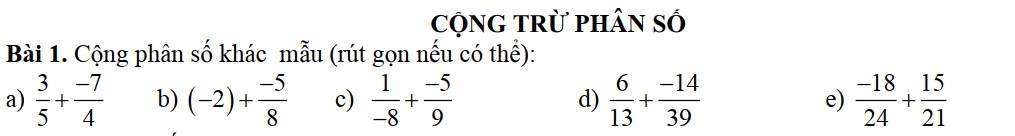
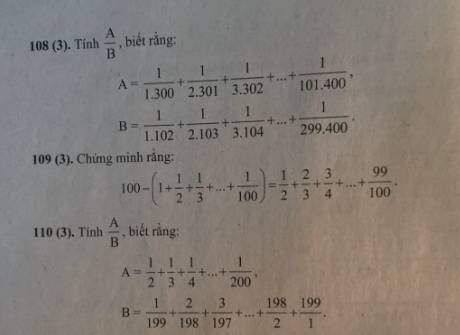
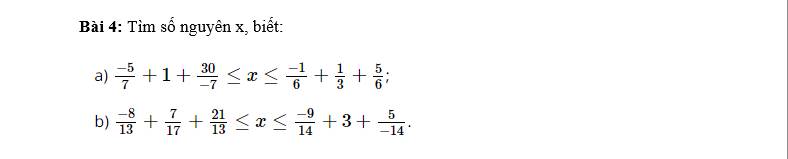
Bài `1`
\(a,35-\left\{12-\left[\left(-14\right)+\left(-2\right)\right]\right\}\\ =35-\left[12-\left(-16\right)\right]\\ =35-\left(12+16\right)\\ =35-28\\ =7\\ b,1997-\left[10\cdot\left(4^3-56\right):2^3+2^3\right]\cdot2023^0\\ =1997-\left[10\cdot\left(64-56\right):8+8\right]\cdot1\\ =1997-\left(10\cdot8:8+8\right)\\ =1997-\left(80:8+8\right)\\ =1997-\left(10+8\right)\\ =1997-18\\ =1979\)
Bài `2`
`124+(118-x)=217`
`=>118-x=217-124`
`=>118-x=93`
`=>x=118-93`
`=>x=25`
`3^(x+2)+3^x=10`
`=>3^x(3^2 +1)=10`
`=> 3^x*10=10`
`=>3^x=1`
`=> x=0`
Bài 5:
\(B=3+3^2+3^3+...+3^{2015}\)
=>\(3B=3^2+3^3+...+3^{2016}\)
=>\(3B-B=3^2+3^3+...+3^{2016}-3-3^2-...-3^{2015}\)
=>\(2B=3^{2016}-3\)
=>\(2B+3=3^{2016}\) là lũy thừa của 3(ĐPCM)
Bài 3:
\(96=2^5\cdot3;120=2^3\cdot3\cdot5;72=2^3\cdot3\)
=>\(ƯCLN\left(96;120;72\right)=2^3\cdot3=24\)
Để phân chia 96 bạn thi Văn, 120 bạn thi Toán và 72 bạn thi Anh ra thành các hàng sao cho mỗi hàng có số bạn thi mỗi môn bằng nhau thì số hàng và số bạn mỗi hàng phải là ước chung của 96;120;72
=>Để số hàng ít nhất số học sinh mỗi hàng là lớn nhất
=>Số hàng ít nhất khi số học sinh mỗi hàng là ƯCLN(72;96;120)=24 bạn/hàng
Số hàng khi đó là:
\(\dfrac{72+96+120}{24}=3+4+5=12\left(hàng\right)\)