Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: Hai góc bù nhau có tổng số đo bằng 1800
Số đo góc xOy là: 1800 - 500= 1300
=> Góc xOy =1300
Ta có: Hai góc bù nhau có tổng số đo bằng 180° Số đo góc xOy là: 180° - 50°= 130°=> Góc xOy =130°

a)Vì tia oy và ox đều nằm trên cùng một bờ là tia ox
Suy ra: xot+toy=xoy
Do đó ot nằm giữa 2 tia ox và oy
b)Vì xot+toy=xoy
Thay số:400+toy=1100
toy=1100-400=700
Vì oz là tia phân giác góc toy
Suy ra: yoz=zot=yot:2=700:2=350
Vì ot nằm giữa góc zox
Suy ra:zot+tox=zox
Thay số:350+400=zox=750
Vậy yot=350;zox=750
c)Tia ot ko phải là tia phân giác vì theo câu b ta được
ot nằm giữa góc zox.
Mà 2 góc do tia ot tạo thành lại là hai góc ko bằng nhau
Do đó tia ot ko phải là tia phân giác

a) Trên cùng 1 nửa mp bờ chứa tia Ox, góc xOt = 60 độ, góc xOy = 130 độ mà xOt < xOy ( vì 60<130 ).
=> Tia Ot nằm giữa 2 tia Ox,Oy. (1)
b) => xOt + tOy = xOy
=> 60 độ + tOy = 130 độ
=> tOy = 130 độ - 60 độ = 70 độ.
c) Vì xOt = 60 độ, tOy = 70 độ. (2)
Từ (1) và (2) => tia Ot ko phải là tia phân giác của góc xOy.
Chúc bạn học giỏi ! Nhớ chọn mình nhé !

B A C H
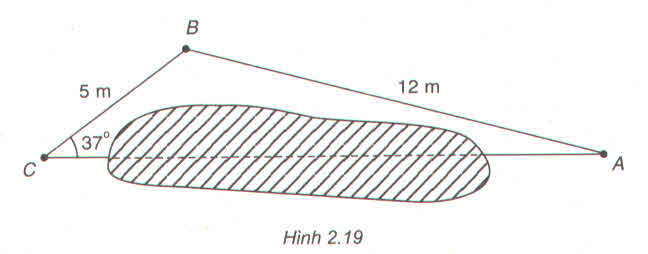
Hạ \(BH\perp AC\).
\(CH=CB.sin37^o\approx3m.\)
Áp dụng định lý Pi-ta-go trong tam giác vuông BCH:
\(BH=\sqrt{AB^2-AH^2}=\sqrt{5^2-3^2}=4m\).
Áp dụng định lý Pi-ta-go trong tam giác vuông BHA:
\(HA=\sqrt{BC^2-BH^2}=\sqrt{12^2-4^2}=8\sqrt{2}m\).
\(AC=AH+HC=8\sqrt{2}+3m\).

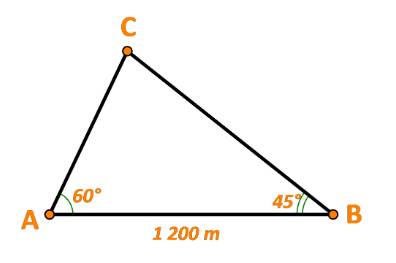
Ta có: \(\widehat C = {180^o} - {60^o} - {45^o} = {75^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow \left\{ \begin{array}{l}AC = \frac{{\sin B.AB}}{{\sin C}}\\BC = \frac{{\sin A.AB}}{{\sin C}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}AC = \frac{{\sin {{45}^o}.1200}}{{\sin {{75}^o}}} \approx 878\\BC = \frac{{\sin {{60}^o}.1200}}{{\sin {{75}^o}}} \approx 1076\end{array} \right.\)
Vậy AC = 878 m, BC = 1076 m.

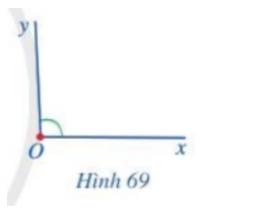
\(\widehat{x'Oy'}=\widehat{xOy}=40^0\)
\(\widehat{xOy'}=180^0-40^0=140^0\)
Do đó: \(\dfrac{\widehat{x'Oy'}}{\widehat{xOy'}}=\dfrac{40^0}{140^0}=\dfrac{2}{7}\)

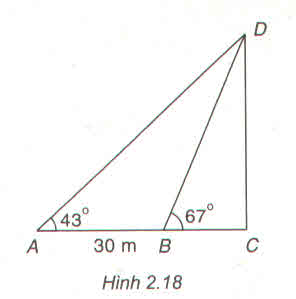
Có:
\(DC=AC.tan43^o=\left(AB+BC\right).tan43^o\).
\(DC=BC.tan67^o\).
Vì vây:
\(\left(AB+BC\right).tan43^o=BC.tan67^o\)
\(\Leftrightarrow BC=\dfrac{AB.tan43^o}{tan67^o-tan43^o}=26,55m\).
Suy ra: \(DC=BC.tan67^o=26,55.tan67^o=62,55m\).
Vậy chiều cao DC của chân tháp là 62,55m.
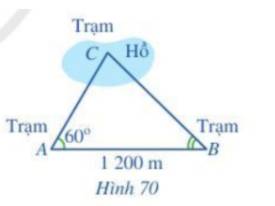
Áp dụng định lí cosin trong tam giác OAB, ta có:
\(\begin{array}{l}\cos O = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}} = \frac{{{2^2} + {2^2} - 3,{1^2}}}{{2.2.2}} \approx - 0,2\\ \Rightarrow \widehat {xOy} \approx {102^o}\end{array}\)