Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

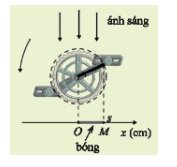
Thanh OM quay được \(3\dfrac{1}{10}\) vòng thì \(\alpha=3\dfrac{1}{10}\cdot360^o=1116^o\)
Từ M kẻ MH \(\perp\) Ox
\(\Rightarrow OH=15\cdot\left|cos1116^o\right|\approx12,1\)
Vậy độ dài bóng O'M' của OM khi thanh quay được \(3\dfrac{1}{10}\) là 12,1cm.

a) Trong 1 giây bánh xe quay được \(\frac{{11}}{5}\) vòng.
Vì 1 vòng bằng \({360^0}\) nên góc mà bánh xe quay được trong 1 giây là:
\(\frac{{11}}{5}{.360^0} = {792^0}\)
Vì 1 vòng bằng \(2\pi \) nên góc mà bánh xe quay được trong 1 giây là:
\(\frac{{11}}{5}.2\pi = \frac{{22\pi }}{5}\;\left( {rad} \right)\)
b) Ta có: 1 phút = 60 giây
Trong 60 giây, bánh xe quay được số vòng: \(\frac{{11}}{5}.60 = 132\) vòng.
Chu vi bánh xe là \(C = 680\pi\) mm
Độ dài quãng đường người đó đi trong 1 phút là: \(680\pi. 132 =89760\pi\) mm

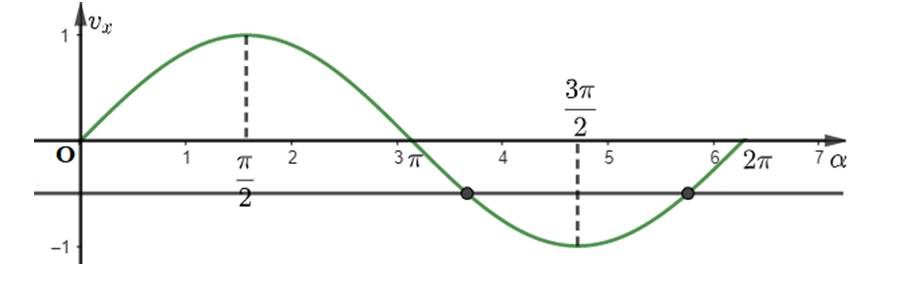
Độ dài bóng OM bằng 10 cm khi s = 10 hoặc s = -10.
Khi s = 10. Ta có: \(17cos5\pi t = 10 \Leftrightarrow cos5\pi t = \frac{{10}}{{17}}\)
Khi s = 10. Ta có: \(17cos5\pi t = - 10 \Leftrightarrow cos5\pi t = \frac{{ - 10}}{{17}}\)
Từ đó, ta có thể xác định được các thời điểm t bằng cách giải phương trình côsin.

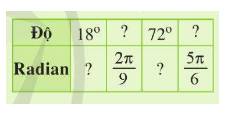
Ta có bảng chuyển đổi số đo độ và số đo radian của một số góc sau:
Độ | \({18^ \circ }\) | \(\frac{{2\pi }}{9}.\frac{{180}}{\pi } = {40^ \circ }\) | \({72^ \circ }\) | \(\frac{{5\pi }}{6}.\frac{{180}}{\pi } = {150^ \circ }\) |
Radian | \(18.\frac{\pi }{{180}} = \frac{\pi }{{10}}\) | \(\frac{{2\pi }}{9}\) | \(72.\frac{\pi }{{180}} = \frac{{2\pi }}{5}\) | \(\frac{{5\pi }}{6}\) |

a) Điểm G là điểm biểu diễn cho góc lượng giác có số đo \(\alpha \). Khi đó tọa độ điểm \(G\left( {3cos\alpha ;{\rm{ }}3sin\alpha } \right)\).
Chiều cao của gàu ở vị trí G đến mặt nước là: \(3{\rm{ }} + {\rm{ }}3sin\alpha \) (m).
b) Khoảng cách của gàu đến mặt nước bằng 1,5m khi \(3 + 3sin\alpha = 1,5 \Leftrightarrow sin\alpha {\rm{ }} = \frac{{ - 1}}{2}\)
Một vòng quay là 30 giây và t nằm trong khoảng từ 0 đến 1 phút do đó t ∈ [0; 2π].

a) Chiều dài một vòng của quỹ đạo là : \(9000.2.\pi \) (km)
Quãng đường vệ tinh đã chuyển động được sau 1 giờ là \(\frac{{9000.2.\pi }}{3} = 6000\pi \)(km)
Quãng đường vệ tinh đã chuyển động được sau 3 giờ là \(18000\pi \)(km)
Quãng đường vệ tinh đã chuyển động được sau 5 giờ là \(\frac{{9000.2.\pi }}{3}.5 = 30000\pi \)(km)
b)Vệ tinh chuyển động được quãng đường 200 000 km sau sô giờ là : \(\frac{{200000}}{{6000\pi }} \approx 11\)(giờ)

Ta nhận xét rằng khi thả bóng thì bóng đi được 1 lược còn kể từ lần nảy đầu tiên đến khi dừng lại thì bóng đi được 2 lược (1 nảy lên và 1 rơi xuống). Giả sử sau lần nảy thứ n + 1 thì bóng dừng hẳn.
Quãng đường bóng đi được tính đến lần chạm sàn thứ nhất là:
\(S_1=63\)
Quãng đường bóng đi được tính đến lần chạm sàn thứ 2 là:
\(S_2=63+63.\dfrac{1^1}{10^1}\)
Quãng đường bóng đi được tính đến lần chạm sàn thứ (n + 1) là:
\(S_{n+1}=63+63.\left(\dfrac{1}{10}+\dfrac{1}{10^2}+...+\dfrac{1}{10^n}\right)\)
\(=63+63.\dfrac{\dfrac{1}{10}}{1-\dfrac{1}{10}}=70\left(m\right)\)
Vậy độ dài hành trình của quả bóng từ thời điểm ban đầu cho đến khi nó nằm yên trên mặt đất là \(70\left(m\right)\)
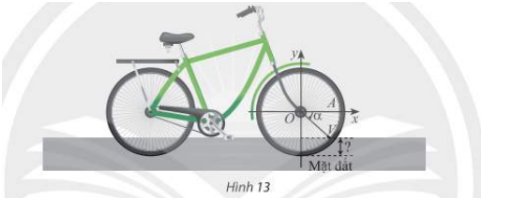




Sau một phút di chuyển, van V đã quay được một góc lượng giác có số đo góc là: \(\alpha=11\cdot60=660\left(rad\right)\)
Khi đó tọa độ điểm V biểu diễn cho góc lượng giác trên có tọa độ là: \(V\left(58\cdot cos\alpha,58\cdot sin\alpha\right)\approx\left(56;15,2\right)\)
Từ đó, khoảng cách từ van đến mặt đất khoảng \(58-15,2\approx42,8\left(cm\right)\)