
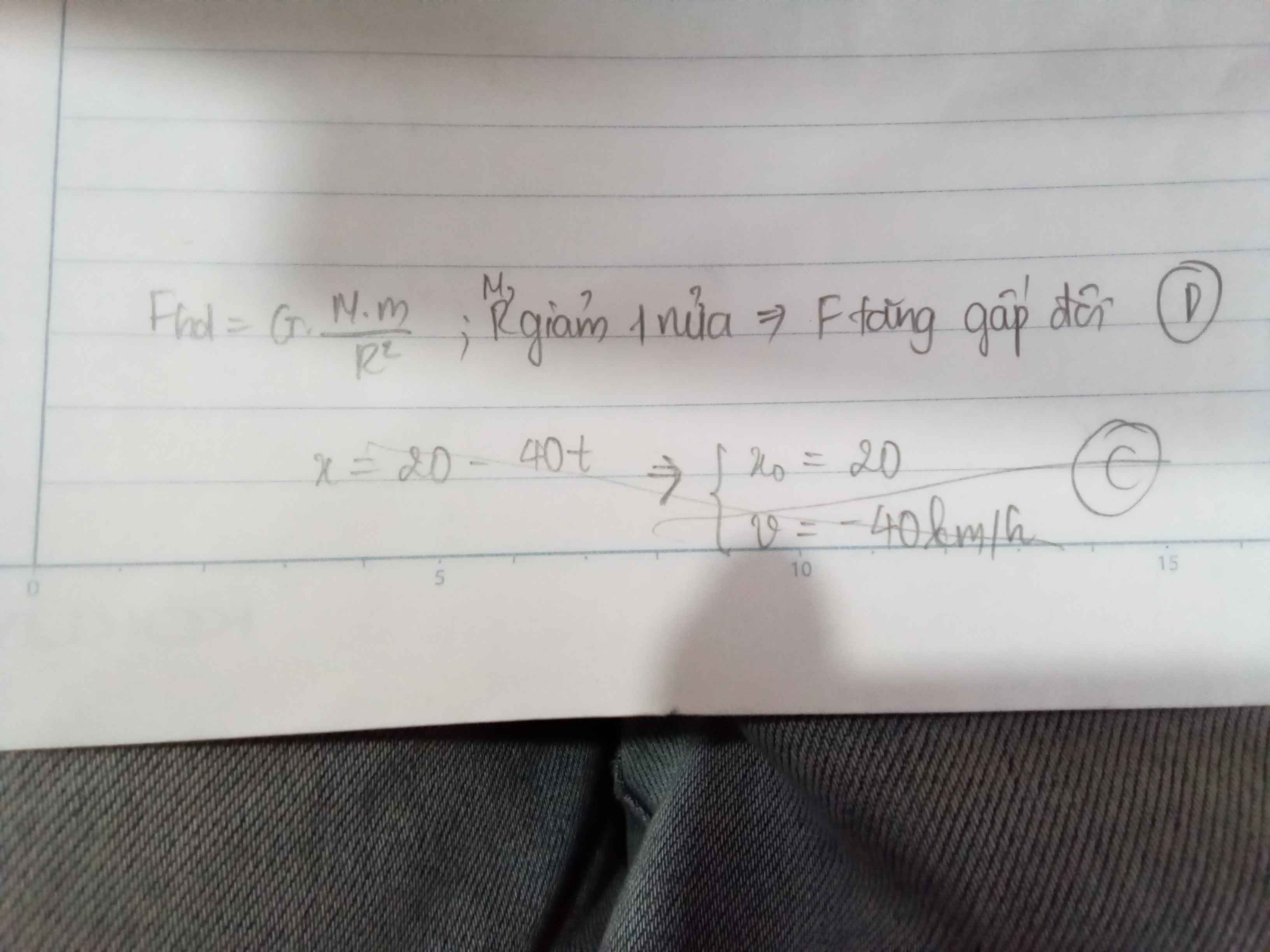
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

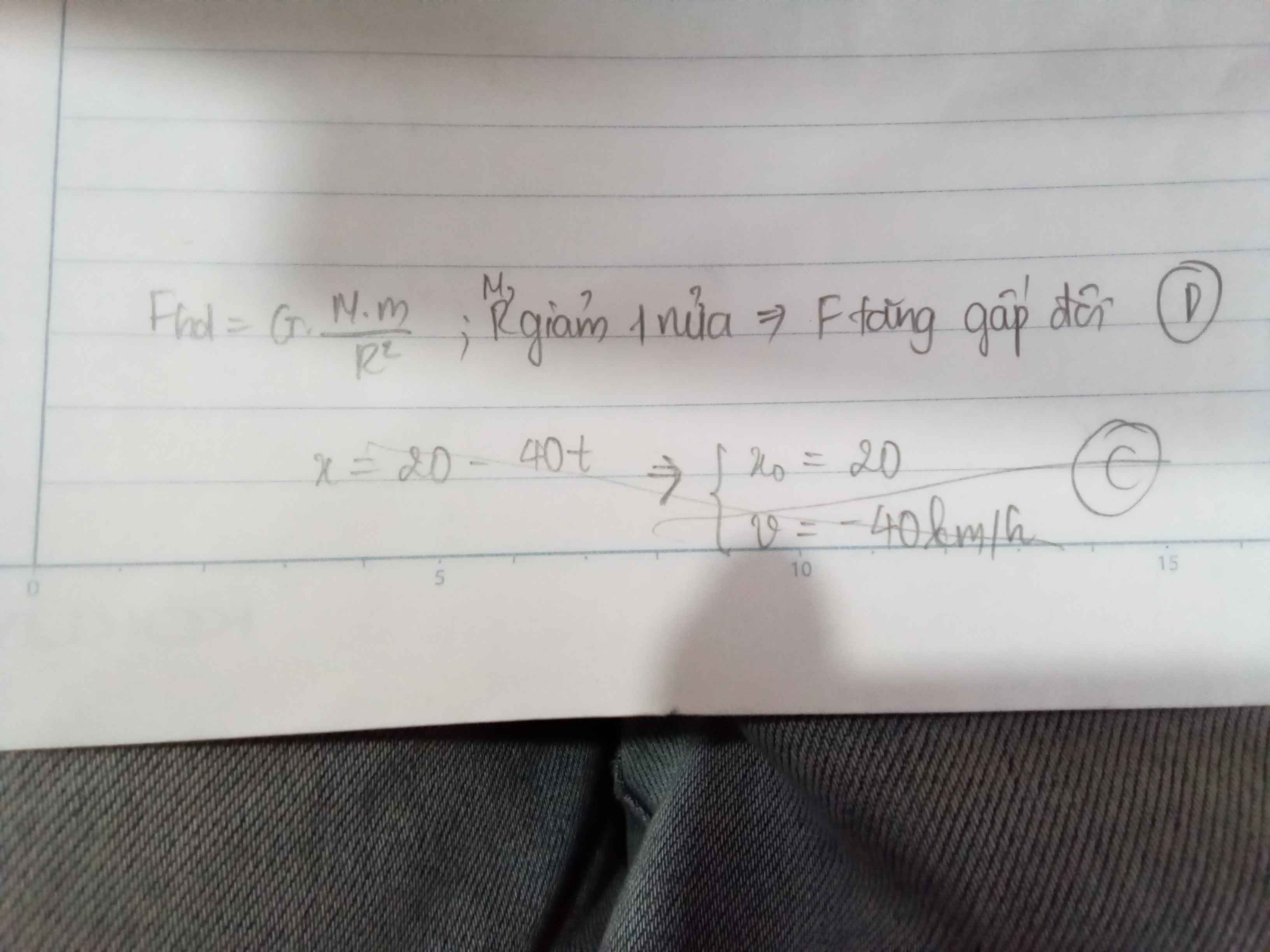

Áp dụng công thức tính lực hấp dẫn:
\(F_{hd}=G\dfrac{m_1.m_2}{R^2}\)
Khi khối lượng và khoảng cách giữa chúng đều giảm đi phân nửa thì ta có:
\(F_{hd}'=G\dfrac{m_1'.m_2'}{R'^2}==G\dfrac{(0,5.m_1).(0,5.m_2)}{(0,5.R)^2}=F_{hd}\)
Do vậy, lực hấp dẫn vẫn giữ nguyên như cũ.
Chọn đáp án C.

Lực hấp dẫn có công thức:
\(F_{hd}=G\cdot\dfrac{m_1\cdot m_2}{R^2}\)
Nếu m tăng gấp đôi và R giảm 2 lần thì độ lớn lực hấp dẫn cũng tăng 8 lần vì:
\(F_{hd}'=G\cdot\dfrac{2m_1\cdot m_2}{\left(\dfrac{R}{2}\right)^2}=G\cdot\dfrac{2m_1\cdot m_2}{\dfrac{1}{4}R^2}=8F_{hd}\)

Chọn D.
Ta có: F h d = G m 1 m 2 r 2
Nếu khối lượng tăng gấp đôi → tử số tăng gấp 4; khoảng cách tăng gấp đôi → mẫu số tăng gấp 4. Lực hấp dẫn không thay đổi.

Đáp án D.
F h d = G m 1 m 2 r 2 khối lượng tăng gấp đôi → tử số tăng gấp 4; khoảng cách tăng gấp đôi → mẫu số tăng gấp 4. Lực hấp dẫn không thay đổi.

giảm
\(F_{hd0}=\dfrac{G.m_1.m_2}{R^2}\)
\(F_{hd1}=\dfrac{\dfrac{G.m_1.m_2}{4}}{\left(R.2\right)^2}=\dfrac{F_{hd0}}{16}\)