Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có 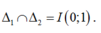
Vì A thuộc ∆1 nên A( a; a+ 1).
Vì P( 2;1) là trung điểm của đoạn AB nên B( 4-a; 1-a).
Mặt khác:
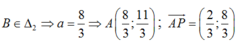
Đường thẳng AP có VTPT ( 4;-1) và qua P(2;1) nên có phương trình:
4x – y- 7 = 0

b: Tọa độ điểm A là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}-x+1=x+1\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
Tọa độ điểm B là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}y=-1\\-x+1=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=2\end{matrix}\right.\)
Tọa độ điểm C là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}y=-1\\x+1=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-1\end{matrix}\right.\)

Sửa đề: AD=AC
a: Xét ΔACE và ΔADE có
AC=AD
\(\widehat{CAE}=\widehat{DAE}\)
AE chung
DO đó: ΔACE=ΔADE
Suy ra: \(\widehat{CAE}=\widehat{DAE}\)
hay AE là phân giác của góc CAB
b: Ta có: AC=AD
EC=ED
DO đó: AE là đường trung trực của CD
c: ta có: AE là đường trung trực của CD
nên AE\(\perp\)CD tại I
=>ΔAID vuông tại I
=>\(\widehat{ADI}< 90^0\)
=>\(\widehat{CDB}>90^0\)(Do góc ADI và góc CDB là hai góc kề bù)
Xét ΔCDB có \(\widehat{CDB}>90^0\)
nên BC là cạnh lớn nhất
=>BC>CD

\(\overrightarrow{AM}.\overrightarrow{AB}=AM^2=\overrightarrow{AM}^2\)
\(\Leftrightarrow\overrightarrow{AM}\left(\overrightarrow{AB}-\overrightarrow{AM}\right)=0\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{MB}=0\)
\(\Rightarrow AM\perp BM\)
\(\Rightarrow\) Quỹ tích là đường tròn đường kính AB

Phương trình hoành độ giao điểm của ∆ và (P) là
x 2 - x + 3 = x + 2 m ⇔ x 2 - 2 x + 3 = 0 (*)
Giả sử A ( x A ; y A ) thì B x B ; y B là các nghiệm của phương trình (*).
Theo định lí Vi-ét ta có x A + x B = 2 .
Ta có y A = x A + 2 m , y B = x B + 2 m nên y A + y B = x A + x B + 4 m = 2 + 4 m .
Tọa độ trung điểm I của đoạn thẳng AB là I x A + x B 2 ; y A + y B 2 = I 1 ; 2 m + 1 .
Chọn A.