TC
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MA
3
24 tháng 8 2021
\(\left(2x+3\right)\left(4x^2-6x+9\right)-8x\left(x^2-2\right)\)
\(=\left(2x+3\right)\left[\left(2x^2\right)-2x.3^2\right]-8x\left(x^2-2\right)\)
\(=\left(2x\right)^3+3^3-8x^3+16x\)
\(=18x^3+27-8x^3+16x\)
\(=16x+27\)
24 tháng 8 2021
(2x + 3)(4x2 - 6x + 9) - 8x(x2 - 2)
= (2x)3 + 33 - 8x(x2 - 2)
= 8x3 + 9 - 8x3 + 16x
= 9 + 16x
Chúc bạn học tốt
DM
0
20 tháng 10 2016
A= (2x-1)2-(2x+3)(x-2)-2(x+2)(x+5)
A= 4x2-4x+1-(2x2-x-6)-2(x2+7x+10)
A=4x2-4x+1-2x2+x+6-2x2-14x-20
A= -17x-13
Thay x= -3, ta có:
A= -17.3-13=-51-13=-64
NH
2
13 tháng 8 2015
(2x+3)^2+(2x+5)^2-2(2x+3)(2x+5)
=(2x+3)^2-2(2x+3)(2x+5)+(2x+5)^2
=(2x+3+2x+5)^2
=(4x+8)^2
31 tháng 10 2020
Bài làm
Như đã nhắn là mình sẽ làm theo quan điểm của mình là 5/(x^2 - 1) nha
\(A=\left[\frac{3\left(x+2\right)}{2x^3+2x+2x^2+2}+\frac{2x^2-x-10}{2x^3-2-2x^2+2x}\right]:\left[\frac{5}{x^2-1}+\frac{3}{2x+2}-\frac{3}{2x-2}\right]\)
\(A=\left[\frac{3\left(x+2\right)}{2x^2\left(x+1\right)+2\left(x+1\right)}+\frac{2x^2+4x-5x-10}{\left(2x^3-2x^2\right)+\left(2x-2\right)}\right]:\left[\frac{5}{x^2-1}+\frac{3}{2\left(x+1\right)}-\frac{3}{2\left(x-1\right)}\right]\)
\(A=\left[\frac{3\left(x+2\right)}{\left(2x^2+2\right)\left(x+1\right)}+\frac{2x\left(x+2\right)-5\left(x+2\right)}{2x^2\left(x-1\right)+2\left(x-1\right)}\right]:\left[\frac{5\cdot2}{2\left(x+1\right)\left(x-1\right)}+\frac{3}{2\left(x+1\right)}-\frac{3}{2\left(x-1\right)}\right]\)
\(A=\left[\frac{3\left(x+2\right)}{\left(2x^2+2\right)\left(x+1\right)}+\frac{\left(2x-5\right)\left(x+2\right)}{\left(2x^2+2\right)\left(x-1\right)}\right]:\left[\frac{5\cdot2}{2\left(x+1\right)\left(x-1\right)}+\frac{3}{2\left(x+1\right)}-\frac{3}{2\left(x-1\right)}\right]\)
\(A=\left[\frac{3\left(x+2\right)\left(x-1\right)}{\left(2x^2+2\right)\left(x^2-1\right)}+\frac{\left(2x-5\right)\left(x+2\right)\left(x+1\right)}{\left(2x^2+2\right)\left(x^2-1\right)}\right]:\left[\frac{5\cdot2}{2\left(x+1\right)\left(x-1\right)}+\frac{3\left(x-1\right)}{2\left(x^2-1\right)}-\frac{3\left(x+1\right)}{2\left(x^2-1\right)}\right]\)
\(A=\left[\frac{3\left(x+2\right)\left(x-1\right)+\left(2x-5\right)\left(x+2\right)\left(x+1\right)}{\left(2x^2+2\right)\left(x^2-1\right)}\right]:\left[\frac{10}{2\left(x^2-1\right)}+\frac{3x-3}{2\left(x^2-1\right)}-\frac{3x+3}{2\left(x^2-1\right)}\right]\)
\(A=\left[\frac{\left(x+2\right)\left[3x-3+\left(2x-5\right)\left(x+1\right)\right]}{\left(2x^2+2\right)\left(x^2-1\right)}\right]:\left[\frac{10+3x-3-3x-3}{2\left(x^2-1\right)}\right]\)
\(A=\left[\frac{\left(x+2\right)\left(3x-3+2x^2+2x-5x-5\right)}{\left(2x^2+2\right)\left(x^2-1\right)}\right]:\frac{4}{2\left(x^2-1\right)}\)
\(A=\frac{\left(x+2\right)\left(2x^2-8\right)}{\left(2x^2+2\right)\left(x^2-1\right)}\cdot\frac{\left(x^2-1\right)}{2}\)
\(A=\frac{\left(x+2\right)2\left(x^2-4\right)}{2\left(2x^2+2\right)}\)
\(A=\frac{2\left(x+2\right)\left(x-2\right)\left(x+2\right)}{4\left(x^2+1\right)}\)
\(A=\frac{\left(x+2\right)^2\left(x-2\right)}{2\left(x^2+1\right)}\)
:>>> Chả biết đúng không nữa nhưng số to quá :>>
CH
Cô Hoàng Huyền
Admin
VIP
21 tháng 12 2017
ĐK: \(\hept{\begin{cases}x\ne1\\x\ne\frac{3}{2}\end{cases}}\)
\(\left(\frac{2x}{2x^2-5x+3}-\frac{5}{2x-3}\right)\div\left(3+\frac{2}{1-x}\right)\)
\(=\frac{2x-5\left(x-1\right)}{\left(2x-3\right)\left(x-1\right)}:\frac{3-3x+2}{1-x}\)
\(=\frac{5-3x}{\left(2x-3\right)\left(x-1\right)}.\frac{1-x}{5-3x}\)
\(=\frac{1}{3-2x}\)
21 tháng 12 2017
\(\left(\frac{2x}{2x^2-5x+3}-\frac{5}{2x-3}\right):\left(3+\frac{2}{1-x}\right)\)\(ĐKXĐ:x\ne1;x\ne\frac{3}{2}\)
\(=\)\(\left[\frac{2x}{\left(2x-3\right)\left(x-1\right)}-\frac{5\left(x-1\right)}{\left(2x-3\right)\left(x-1\right)}\right]:\left[\frac{3x-3-2}{x-1}\right]\)
\(=\frac{2x-5x+5}{\left(2x-3\right)\left(x-1\right)}:\frac{3x-5}{x-1}\)
\(=\frac{-3x+5}{\left(2x-3\right)\left(x-1\right)}.\frac{x-1}{3x-5}\)
\(=\frac{-\left(3x-5\right)}{2x-3}.\frac{1}{3x-5}\)
\(=\frac{-1}{2x-3}\)
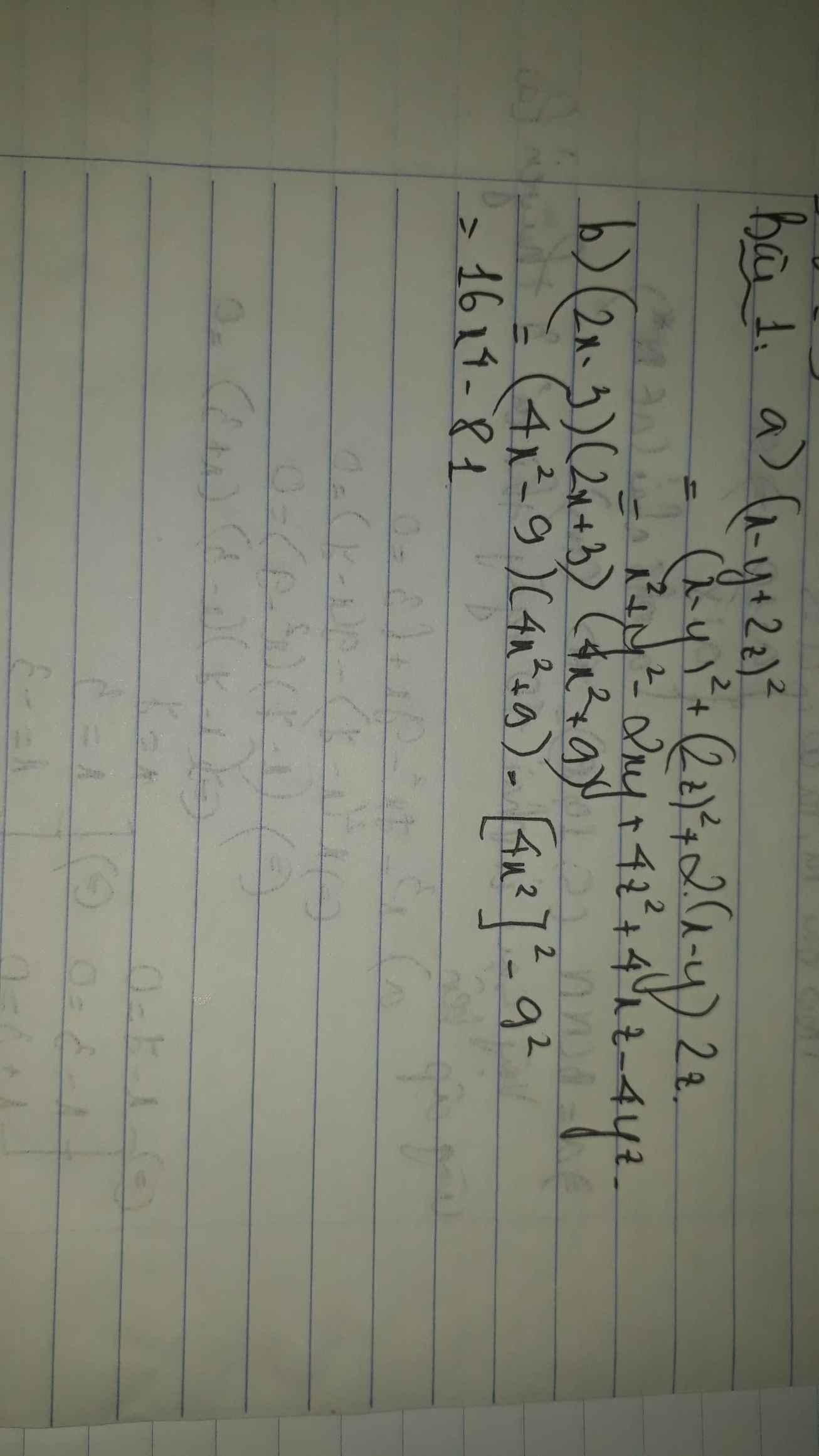
mình nhầm tí.
\(=\left(2x-3-2x-5\right)^2=\left(-8\right)^2=64\) nha