Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Còn một cái nữa là ta có thể so sánh với số trung gian như 1 và 0 .
Vì a/b=c/d khi a.c=b.d
Giờ thì mình kết thúc bài làm.

Theo phương pháp so sánh hai phân số có cùng mẫu số mà chúng ta đã
được học thì bạn Liên giải thích đúng, còn Oanh giải thích sai.
Ví dụ cho thấy bạn Oanh sai : hai phân số 3/8 và 1/2 có 3 lớn hơn 1 còn 8
lớn hơn 2 nhưng 3/8 nhỏ hơn 1/2 vì khi quy đồng về mẫu số chung là 8 thì
ta có: \(\dfrac{1}{2}=\dfrac{4}{8}>\dfrac{3}{8}\)

a. \(\dfrac{-3}{5}\)
b. \(\dfrac{-2}{3}\) c. \(\dfrac{4}{39}\) d. \(\dfrac{26}{45}\)

a: \(\dfrac{5}{24}< \dfrac{15}{24}=\dfrac{5}{8}\)
b: \(\dfrac{6+9}{6\cdot9}=\dfrac{15}{54}\)
4/9=24/54
2/3=36/54
Do đó: \(\dfrac{15}{54}< \dfrac{24}{54}< \dfrac{36}{54}\)

a, \(A-B=\frac{3}{8^3}+\frac{7}{8^4}-\frac{7}{8^3}-\frac{3}{8^4}==\left(\frac{7}{8^4}-\frac{3}{8^4}\right)-\left(\frac{7}{8^3}-\frac{3}{8^3}\right)=\frac{4}{8^4}-\frac{4}{8^3}< 0\)
Vậy A < B
b, \(A=\frac{10^7+5}{10^7-8}=\frac{10^7-8+13}{10^7-8}=1+\frac{13}{10^7-8}\)
\(B=\frac{10^8+6}{10^8-7}=\frac{10^8-7+13}{10^8-7}=1+\frac{13}{10^8-7}\)
Vì \(10^7-8< 10^8-7\Rightarrow\frac{1}{10^7-8}>\frac{1}{10^8-7}\Rightarrow\frac{13}{10^7-8}>\frac{13}{10^8-7}\Rightarrow A>B\)
c,Áp dụng nếu \(\frac{a}{b}>1\Rightarrow\frac{a}{b}>\frac{a+n}{a+n}\) có:
\(B=\frac{10^{1993}+1}{10^{1992}+1}>\frac{10^{1993}+1+9}{10^{1992}+1+9}=\frac{10^{1993}+10}{10^{1992}+10}=\frac{10\left(10^{1992}+1\right)}{10\left(10^{1991}+1\right)}=\frac{10^{1992}+1}{10^{1991}+1}=A\)
Vậy A < B

c: \(\left|\dfrac{7}{5}x+\dfrac{2}{3}\right|=\left|\dfrac{4}{3}x-\dfrac{1}{4}\right|\)
=>7/5x+2/3=4/3x-1/4 hoặc 7/5x+2/3=1/4-4/3x
=>1/15x=-11/12 hoặc 41/15x=-5/12
=>x=-55/4 hoặc x=-25/164
d: |7/8x+5/6|=|1/2x+5|
=>|42x+40|=|24x+240|
=>42x+40=24x+240 hoặc 42x+40=-24x-240
=>18x=200 hoặc 66x=-280
=>x=100/9 hoặc x=-140/33

Vì nếu lấy \(\dfrac{2}{5}\) số cam giỏ thứ \(1\), \(\dfrac{1}{4}\) giỏ thứ \(2\) và \(\dfrac{5}{12}\) giỏ thứ \(3\) thì được \(64\) quả.
Nên nếu lấy \(4.\dfrac{2}{5}=\dfrac{8}{5}\) số cam giỏ thứ \(1\),\(4.\dfrac{1}{4}=1\) giỏ thứ \(2\) và \(4.\dfrac{5}{12}=\dfrac{5}{3}\) giỏ thứ thì được \(4.64=256\) (quả)
Như vậy nếu lấy \(\dfrac{8}{5}\) số cam giỏ thứ \(1\), giỏ thứ \(2\) và \(\dfrac{5}{3}\) giỏ thứ \(3\) thì được \(256\) quả.
Mà ba giỏ cam có tất cả \(172\) quả. Nên nếu lấy \(\dfrac{8}{5}-1=\dfrac{3}{5}\) số cam giỏ thứ \(1\) và \(\dfrac{5}{3}-1=\dfrac{2}{3}\) số cam giỏ thứ \(3\) thì được \(256-172=84\) quả.
Hay nếu lấy \(\dfrac{3}{5}\) số cam giỏ thứ \(1\) và \(\dfrac{2}{3}\) số cam giỏ thứ \(3\) thì được \(84\) quả.
Do đó, nếu lấy \(\dfrac{3}{5}:3=\dfrac{1}{5}\) số cam giỏ thứ \(1\) và \(\dfrac{2}{3}:3=\dfrac{2}{9}\) số cam giỏ thứ \(3\) thì được \(84:3=24\) quả.
Vậy nếu lấy \(\dfrac{1}{5}\) số cam giỏ thứ \(1\) và \(\dfrac{2}{9}\) số cam giỏ thứ \(3\) thì được \(28\) quả.

a) \(\dfrac{-1}{-4}\)=\(\dfrac{1}{4}>0\)
\(\dfrac{3}{-4}< 0\)
\(\Rightarrow\dfrac{1}{4}>\dfrac{3}{-4}hay\dfrac{-1}{-4}>\dfrac{3}{-4}\)
b) Ta có:
\(\dfrac{15}{17}=1-\dfrac{2}{17}\\ \)
\(\dfrac{25}{27}=1-\dfrac{2}{27}\\ \\ \)
Mà \(\dfrac{2}{17}>\dfrac{2}{27}\left(17< 27\right)\)
\(\Rightarrow1-\dfrac{2}{17}< 1-\dfrac{2}{27}\)hay \(\dfrac{15}{17}< \dfrac{25}{27}\)
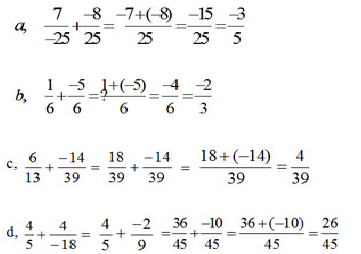
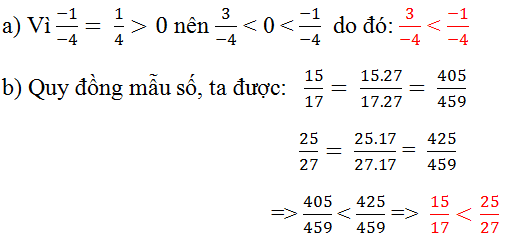
-5/6<0<3/4
-5/6<0<3/4