Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,\(M=\left(\frac{4}{x-4}-\frac{4}{x+4}\right).\frac{x^2+8x+16}{32}\)
\(M=\left(\frac{4\left(x+4\right)-4\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}\right).\frac{\left(x+4\right)^2}{32}\)
\(M=\frac{4x+16-4x+16}{\left(x+4\right)\left(x-4\right)}.\frac{\left(x+4\right)^2}{32}\)
\(M=\frac{32\left(x+4\right)^2}{32\left(x+4\right)\left(x-4\right)}=\frac{x+4}{x-4}\)
b,
Để M = \(\frac{1}{3}\)
\(\Rightarrow x-4=3x+12\)
\(\Rightarrow2x=16\Leftrightarrow x=8\)
\(c,\)\(\frac{x+4}{x-4}=\frac{x-4+8}{x-4}\)
\(\Rightarrow x-4\inƯ\left(8\right)=\left(1;-1;2;-2;4;-4;8;-8\right)\)
\(\Rightarrow x-4\in\left(5;3;6;2;8;0;12;-4\right)\)
Vậy để M thuộc Z thì x phải thỏa mãn các điều kiện trên .

a, \(\frac{x^{32}+x^{16}+1}{x^{16}+x^8+1}\)
\(=\frac{x^8+x^4+1}{x^4+x^2+1}\) Vậy phân thức \(a=\frac{x^8+x^4+1}{x^4+x^2+1}\)
P/s; Căn thức a, là phân số tối giản
b, \(\frac{x^8+3x^4+4}{x^4+x^2+2}\)
\(=\frac{x^4+3x^2+2}{x^2+x^1+1}\) Vậy căn thức \(b=\frac{x^4+3x^2+2}{x^2+x^1+1}\)
P/s; Căn thức b, có thể rút gọn được cho 2 và 4
Em ko chắc đâu nhé *-*

Bạn viết biểu thức A ra đi rồi bọn mình mới làm được chứ -.-
Đk : \(x\ne\pm3\)
Để B>A
\(\Leftrightarrow\frac{3}{x+3}>4\)
Rõ ràng: \(x+3>0\)
\(\Rightarrow\frac{3}{x+3}>4\)
\(\Leftrightarrow3>4\left(x+3\right)\)
\(\Leftrightarrow3>4x+12\)
\(\Leftrightarrow-9>4x\)
\(\Leftrightarrow x< \frac{-9}{4}\)
KL: \(x\in Z,x< \frac{-9}{4},x\ne\pm3\)

Rút gọn : \(P=\left(\frac{1}{x-2}-\frac{1}{x+2}+1\right):\frac{1}{x^2-4}\)
\(P=\left(\frac{x+2}{x^2-4}-\frac{x-2}{x^2-4}+\frac{\left(x+2\right)\left(x-2\right)}{x^2-4}\right):\frac{1}{x^2-4}\)
\(P=\frac{x+2-x+2+x^2-4}{x^2-4}:\frac{1}{x^2-4}\)
\(P=\frac{x^2}{x^2-4}.\frac{x^2-4}{1}\)
\(P=x^2\)
........
mk chỉ biết làm rút gọn thôi nha
Điều kiện xác định là
Ta có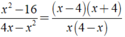
Chọn đáp án C.