Kết quả của rút gọn biểu thức 6 x 2 y 2 8 x y 5 là ?
A. 6 8
B. 3 x 4 y 3
C. 2 x y 2
D. x 2 y 2 x y 5

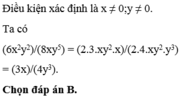
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Kết quả của rút gọn biểu thức 6 x 2 y 2 8 x y 5 là ?
A. 6 8
B. 3 x 4 y 3
C. 2 x y 2
D. x 2 y 2 x y 5

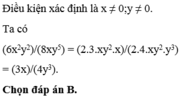



\(P=\left(x-y\right)^2+\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)-4x^2=\left(x-y-x-y\right)^2-\left(2x\right)^2=\left(-2y\right)^2-\left(2x\right)^2\)
\(=\left(2y-2x\right)\left(2y+2x\right)=2\left(y-x\right)2\left(y+x\right)=4\left(x+y\right)\left(y-x\right)\)
\(x^3-x^2y+3x-3y=x^2\left(x-y\right)+3\left(x-y\right)=\left(x-y\right)\left(x^2+3\right)\)
\(x^3-2x^2-4xy^2+x=x\left(x^2-2x+1-4y^2\right)=x\left[\left(x-1\right)^2-\left(2y\right)^2\right]=x\left(x+2y-1\right)\left(x-2y-1\right)\)
\(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-8=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-8\)
Đặt \(x^2+7x+10=t\), ta có:
\(t\left(t+2\right)-8=t^2+2t-8=t^2-2t+4t-8=t\left(t-2\right)+4\left(t-2\right)=\left(t-2\right)\left(t+4\right)\)
\(=\left(x^2+7x+10+4\right)\left(x^2+7x+10-2\right)=\left(x^2+7x+14\right)\left(x^2+7x-8\right)\)

Bài 1. Rút gọn:
\(a, x\left(1-x\right)+6\left(x+3\right)\left(x+3\right)\)
\(=x-x^2+6\left(x^2+6x+9\right)\)
\(=x-x^2+6x^2+36x+54\)
\(=5x^2+37x+54\)
\(b, \left(2-3x\right)\left(2+3x\right)-\left(x+5\right)\left(x-5\right)\)
\(=\left(4-9x^2\right)-\left(x^2-25\right)\)
\(=-10x^2+29\)
\(c, \left(3x+1\right)\left(x+5\right)-\left(x-1\right)\left(x+1\right)\)
\(=3x^2+15x+x+5-x^2+1\)
\(=2x^2+16x+6\)
\(d,\left(2-3x\right)\left(2x+3\right)+6\left(x-1\right)^2\)
\(=\left(4x+6-6x^2-9x\right)+6\left(x^2-2x+1\right)\)
\(=4x+6-6x^2-9x+6x^2-12x+6\)
\(=-17x+12\)
\(e, x\left(5-x\right)-\left(2x+2\right)\left(3x+2\right)-\left(x-2\right)\left(x+2\right)\)
\(=5x-x^2-\left(6x^2+4x+6x+4\right)-\left(x^2-4\right)\)
\(=5x-x^2-6x^2-4x-6x-4-x^2+4\)
\(=-8x^2-5x\)
Bài 2:
a: VT\(=x^3-xy+x^2y^2-y^3-x^3+y^3-x^2y^2\)
=-xy
b: \(VT=x^2+6xy+9y^2-x^2+9y^2-6xy=18y^2=VP\)

Mạn phép bỏ câu a :))
b) a2(b2 - a2) + b2(b2 + a2)
= a2.b2 + a2.(-a2) + b2.b2 + b2.a2
= a2.b2 - a4 + b4 + a2.b2
= a4 + 2a2b2 + b2 (hđt)
c) x2(x3 + 2y - x2y) - y(x2 - x4 + y)
= x2.x3 + x2.2y + x2.(-x2y) + (-y).x2 + (-y).(-x)4 + (-y).y
= x5 + 2x2y - x4y - x2y + x4y - y2
= x5 + (2xy2 - xy2) + (-x4y + x4y) - y2
= x5 + xy2 - y2

a)Ta có: x(x-y) + y(x+y)
= x2-xy+xy+y2
=x2+y2
Thay x=-6 và y=8 vào biểu thức ta được:
(-6)2+82=36+64=100
Vậy tại x=-6 và y=8 thì giá trị biểu thức là 100

a)(x+y)3-3xy(x+y)
\(=\left(x+y\right)\left(x^2+xy+y^2\right)-3xy\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2+xy+y^2-3xy\right)\)
\(=\left(x+y\right)\left(x^2-2xy+y^2\right)\)
c)\(\left(a+b\right)^2-\left(a-b\right)^2-4ab\)
\(=\left[\left(a+b\right)-\left(a-b\right)\right]\left[\left(a+b\right)+\left(a-b\right)\right]-4ab\)
\(=\left(a+b-a+b\right)\left(a+b+a-b\right)-4ab\)
\(=2b.2a-4ab\)
\(=4ab-4ab=0\)

a) Ta có: \(A=x^3+6x^2+12x+8\)
\(=x^3+3\cdot x^2\cdot2+3\cdot x\cdot2^2+2^3\)
\(=\left(x+2\right)^3\)
Thay x=8 vào biểu thức \(A=\left(x+2\right)^3\), ta được:
\(A=\left(8+2\right)^3=10^3=1000\)
Vậy: 1000 là giá trị của biểu thức \(A=x^3+6x^2+12x+8\) tại x=8
b) Ta có: \(B=x^3-3x^2+3x-1\)
\(=x^3-3\cdot x^2\cdot1+3\cdot x\cdot1^2-1^3\)
\(=\left(x-1\right)^3\)
Thay x=101 vào biểu thức \(B=\left(x-1\right)^3\), ta được:
\(B=\left(101-1\right)^3=100^3=1000000\)
Vậy: 1000000 là giá trị của biểu thức \(B=x^3-3x^2+3x-1\) tại x=101
c) Ta có: \(C=\left(\frac{x}{2}-y\right)^3-6\left(y-\frac{x}{2}\right)^2-12\left(y-\frac{x}{2}\right)-8\)
\(=\left(\frac{x}{2}-y\right)^3-6\cdot\left(\frac{x}{2}-y\right)^2+12\cdot\left(\frac{x}{2}-y\right)-8\)
\(=\left(\frac{x}{2}-y-2\right)^3\)
Thay x=4 và y=2 vào biểu thức \(C=\left(\frac{x}{2}-y-2\right)^3\), ta được:
\(C=\left(\frac{4}{2}-2-2\right)^3=\left(2-2-2\right)^3=\left(-4\right)^3=-64\)
Vậy: -64 là giá trị của biểu thức \(C=\left(\frac{x}{2}-y\right)^3-6\left(y-\frac{x}{2}\right)^2-12\left(y-\frac{x}{2}\right)-8\) tại x=4 và y=2

\(P=\frac{x\left(x+5\right)+y\left(y+5\right)+2\left(xy-3\right)}{x\left(x+6\right)+y\left(y+6\right)+2xy}\)
\(=\frac{x^2+5x+y^2+5y+2xy-6}{x^2+6x+y^2+6y+2xy}\)
\(=\frac{\left(x+y\right)^2+5\left(x+y\right)-6}{\left(x+y\right)^2+6\left(x+y\right)}\)
\(=\frac{\left(x+y\right)\left(x+y+5\right)-6}{\left(x+y\right)\left(x+y+6\right)}\)
\(=\frac{2005\times\left(2005+5\right)-6}{2005\times\left(2005+6\right)}\)
\(=\frac{2005\times2010-6}{2005\times2011}\)
\(=\frac{2004}{2005}\)

a) x(x - y) + y (x + y) = x2 – xy +yx + y2= x2+ y2
với x = -6, y = 8 biểu thức có giá trị là (-6)2 + 82 = 36 + 64 = 100
b) x(x2 - y) - x2 (x + y) + y (x2– x) = x3 – xy – x3 – x2y + yx2 - yx
= -2xy
Với x = \(\dfrac{1}{2}\), y = -100 biểu thức có giá trị là -2 . \(\dfrac{1}{2}\) . (-100) = 100.
a)x(x-y)+y(x+y)=x2-xy+xy+y2=x2+y2
Tại x=-6 y=8 ta được :
(-6)2+82=36+64=100
b) x(x2-y)-x2(x+y)+y(x2-x)
=x3-xy-x3-x2y+x2y-xy=-2xy
Tại x=\(\dfrac{1}{2}\) y=-100 ta được :
(-2).\(\dfrac{1}{2}\).(-100)=-1.-100=100

\(A=\left(x+y\right)^2-2xy=25-12=13\)
\(B=\left(x+y\right)\left(x^2+y^2-xy\right)=\left(x+y\right)\left[\left(x+y\right)^2-3xy\right]=5\left(25-18\right)=35\)
\(C=x^2-y^2\Rightarrow C^2=x^4+y^4-2x^2y^2=\left(x^2+y^2\right)^2-4x^2y^2\)
\(C^2=\left[\left(x+y\right)^2-2xy\right]^2-4\left(xy\right)^2=\left(25-12\right)^2-4.36=25\Rightarrow C=\pm5\)
\(D=\frac{x^2+y^2}{xy}=\frac{\left(x+y\right)^2-2xy}{xy}=\frac{25-12}{6}=\frac{13}{6}\)