Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
Xét ΔADF và ΔEDC có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: AF=CE

A B C M N I E
a)
*AMN cân
Vì t/g ABC cân tại A (gt)
=>^B=^C
Do đó: ^ABM=^ACN
Xét t/ABM và t/gACN có
góc ^A chung
AB=AC ( vì t/g ABC cân)
^ABM=^ACN (cmt)
Nên t/gABM=t/gACN (g.c.g)
=>AM=AN (2 cạnh tương ứng = nhau)
=> tam giác ANM cân
*MN//BC
Từ tam giác ANM cân nên => ^A+^ANM+^AMN=180o
tam giác ABC cân nên=>^A+^B+^C=180o
Mà ^B=^C
^ANM=^AM
Nên: ^C=^ANM
=>^MCN=^ANM
Mà 2 góc này lại ở vị trí so le trong
Do đó MN//BC (đpcm)
b)
Vì t/g ABC cân tại A
^ABC=^ACB
Mà BM là tia p/g của ^ABC
CN là tia p/g của ^ACB
do đó: ^MBC=^NCB
=> tam giác EBC cân tại E
Xét t/g AEB và t/g AEC có:
AB=AC (vì t/g ABC cân)
^ABM=^ACN (cmt)
=BE=CE (EBC cân)
=> t/gAEB=t/gAEC(c.g.c)
=>^BAE=^CAE (2 góc tương ứng = nhau)
Do đó AE là tia phân giác của t/gBAC (1)
Xét t/g AIB và t/gAIC có
AB=AC ( vì t/g ABC cân)
IB=IC (I là trung điểm BC)
=>tam giác AIB=t/gAIC (c.g.c)
=>^IAB=^IAC (2 góc tương ứng = nhau)
Do đó:AI là tia phân giác của ^BAC (2)
Từ (1) và (2) => A,I,E thằng hàng ( 2 tia phân giác của 1 góc thì thẳng hàng).

A C B H M N I
a) Xét ΔAMH và ΔNMB:
- MB=MH(M là trung điểm BH)
- Góc HMA= Góc BMN
- MA=MH(gt)
Vậy ΔAMH = ΔNMB(c.g.c)
Suy ra Góc AHM= Góc MBN(2 góc tương ứng)
Mà Góc AHM=90o(AH là đường cao ΔABC)
Nên Góc MBN=90o
Vậy NB vuông góc với BC
b) Ta có: ΔAMH = ΔNMB(cmt)
Nên AH=NB
Vì AH là đường cao ΔABC cân tại A
Nên AH<AB
Vì AH<AB(cmt)
Mà AH=NB
Nên NB<AB
c) và d) bạn đợi tí nhé

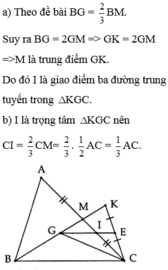
A B C M D E K F I
a) Gọi tia phân giác của ∠BAC cắt DE tại K
Vì AK ⊥ DE ( gt )
=> △ ADK vuông tại K và △ AEK vuông tại K
Xét tam giác vuông ADK và tam giác vuông AEK có:
AK chung
∠ A1 = ∠ A2 ( AK là tia phân giác của ∠ BAC )
=> △ ADK = △ AEK (g.c.g )
=> AD = AE ( 2 cạnh tương ứng )
=> △ ADE cân tại A
Vì BF // AC ( gt )
=> ∠ BFD = ∠AEF ( 2 góc đồng vị ) ( 1 )
Ta có ∠ D = ∠AEF ( △ ADE cân tại A ) ( 2 )
Từ (1) và (2) => ∠ BFD = ∠D
=> △ BDF cân tại B
b) Vì BF // AC ( gt )
=> ∠ MBF = ∠ ECM ( 2 góc so le trong )
Xét tam giác BMF và tam giác EMC có:
∠MBF = ∠ECM ( cmt )
MB = MC ( M là t/ đ BC )
∠ BMF = ∠ EMC ( 2 góc đối đỉnh )
=> △ BMF = △ EMC ( g.c.g )
=> MF = ME ( 2 cạnh tương ứng )
Mà M nằm giữa 2 điểm F và E
=> M là t/đ của EF.
c) Trên tia CA lấy I sao cho IE = IC
Mà CE = BD ( △ BMF = △ EMC )
=> CE = EI = BD
=> IC = EI = BD + BD = 2BD
AC - AI = IC = 2BD
AB = AD - BD
AI = AE - IC
Mà AD = AE ( △ ADE cân tại A )
Và BD = IE ( cmt )
=> AB = AI
Mà AC - AI = AB
=> AC - AB = 2BD.
Chúc bn học tốt nha ! ❤❤
ai rảnh toán thì giúp mình nha . Đây là đề của Sở GDĐT tỉnh Nam Định thi toán 7 cuối năm