
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b) B = 1 + 1x2 + 1x2x3 + 1x2x3x4 + 1x2x3x4x5 +...+ 1x2x3x..x2015
Nhận xét: từ số hạng 1x2x3x4x5 đến 1x2x3x..x2015, mỗi số hạng luôn chứ 2 thừa số 2,5 nên số tận cùng của mỗi số hạng đó là 0
B = 1 + ..2 + ...6 + ...4 = ...2 (những hạng tử có dấu ... nhớ gạch ngang trên đầu)
Vậy B có tận cùng là 2
c) C = 1x3 + 1x3x5 + 1x3x5x7 + ... + 1x3x5x7x..x2015
Nhận xét: Từ số hạng 1x3x5 đến số hạng 1x3x5x7x..x2015 luôn chứa thừa số 5 nên tận cùng nhưng số hạng này là 5 (do những số hạng này là tích của những số lẻ)
Từ số hạng 1x3x5 đến số hạng 1x3x5x7x..x2015 có tất cả (2015 - 5) : 2 + 1 = 1006 số hạng => tận cùng của 1x3x5 + 1x3x5x7 + ... + 1x3x5x7x..x2015 là 1006 x 5 = ...0
=> C = 1x3 + ...0 = ...3
Vậy C tận cùng là 3


Trả lời bằng Tiếng Việt nhé.
Bài 1.
Nếu đi với vận tốc \(50m/min\)thì sẽ đến trường muộn hơn đi với vận tốc \(60m/min\)số phút là:
\(2+1=3\)(phút)
Mỗi mét đi với vận tốc \(50m/min\)hết số phút là:
\(1\div50=\frac{1}{50}\)(phút)
Mỗi mét đi với vận tốc \(60m/min\)hết số phút là:
\(1\div60=\frac{1}{60}\)(phút)
Mỗi mét đi với vận tốc \(60m/min\)nhanh hơn mỗi mét đi với vận tốc \(50m/min\)số phút là:
\(\frac{1}{50}-\frac{1}{60}=\frac{1}{300}\)(phút)
Quãng đường từ nhà đến trường dài:
\(3\div\frac{1}{300}=900\left(m\right)\)
Bài 2.
Để lấy được ít nhất \(20\)cái bút cùng màu thì ta cần lấy ra hết số bút có ít hơn \(20\)cái, số bút có từ \(20\)cái trở lên ta lấy mỗi loại \(19\)cái, sau đó ta lấy thêm \(1\)cái nữa thì chắc chẵn sẽ được ít nhất \(20\)cái bút có cùng màu.
Số bút ít nhất cần lấy ra là:
\(8+12+19+19+1=59\)(cái)

S = 1 x 2 x 3 x 4 x ....... x 300
S = ( 300 : 1 ) : ( 2 x 4 )
S = 37,5
Ta thấy 300 không chia được ra số có dư nên ta gạch 2 và 4


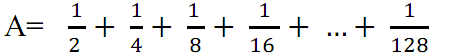 làm hộ nha mn
làm hộ nha mn
























 Các bạn giải giúp Mk nha. Hơi nhiều nhỉ? 5 bạn đầu tiên trả lời cho Mk thì mình Tick cho nha! CẢM ƠN CÁC BẠN RẤT RẤT NHIỀU!
Các bạn giải giúp Mk nha. Hơi nhiều nhỉ? 5 bạn đầu tiên trả lời cho Mk thì mình Tick cho nha! CẢM ƠN CÁC BẠN RẤT RẤT NHIỀU!






 các bạn làm câu e và g với bài 2 là được
các bạn làm câu e và g với bài 2 là được
\(A=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{16}+\dfrac{1}{16}+...-\dfrac{1}{128}\)
\(A=1-\dfrac{1}{128}=\dfrac{127}{128}\)